Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: tan77° - cot63° + sin57° - Mathematics

Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: tan77° - cot63° + sin57°

Sum

tan77° - cot63° + sin57°
= tan(90° - 13°) - cot(90° - 27°) + sin(90° - 33°)
= cot13° - tan27° + cos33°.

shaalaa.com

Trigonometric Equation Problem and Solution

Is there an error in this question or solution?

Chapter 27: Trigonometrical Ratios of Standard Angles - Exercise 27.3

Chapter 27 Trigonometrical Ratios of Standard Angles
Exercise 27.3 | Q 4.4

If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.

Solve for x : 2 cos (3x - 15°) = 1

Solve for x : tan² (x - 5°) = 3

If A = B = 60°, verify that: sin(A - B) = sinA cosB - cosA sinB

Find the value of: `sqrt((1 - sin^2 60°)/(1 + sin^2 60°)` If 3 tan²θ - 1 = 0, find the value
a. cosθ
b. sinθ

Find lengths of diagonals AC and BD. Given AB = 24 cm and ∠BAD = 60°.

In the given figure, ∠B = 60°, ∠C = 30°, AB = 8 cm and BC = 24 cm. Find:
a. BE
b. AC

In the given figure; ∠B = 90°, ∠ADB = 30°, ∠ACB = 45° and AB = 24 m. Find the length of CD.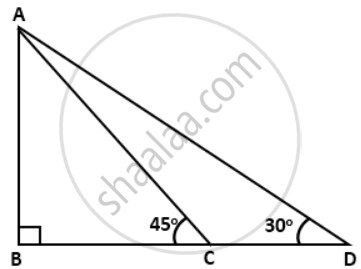

Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos72° - cos88°

Evaluate the following: cos39° cos48° cos60° cosec42° cosec51°