Advertisements
Advertisements
Question
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos72° - cos88°
Solution
cos72° - cos88°
= cos(90° - 18°) - cos(90° - 2°)
= sin18° - sin2°.
APPEARS IN
RELATED QUESTIONS
Solve the following equation for A, if tan 3 A = 1
Calculate the value of A, if (sec 2A - 1) (cosec 3A - 1) = 0
Calculate the value of A, if cos 3A. (2 sin 2A - 1) = 0
Find the value of 'A', if cosec 3A = `(2)/sqrt(3)`
If A = B = 60°, verify that: tan(A - B) = `(tan"A" - tan"B")/(1 + tan"A" tan"B"")`
In a trapezium ABCD, as shown, AB ‖ DC, AD = DC = BC = 24 cm and ∠A = 30°. Find: length of AB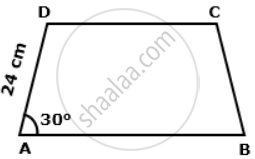
Find x and y, in each of the following figure: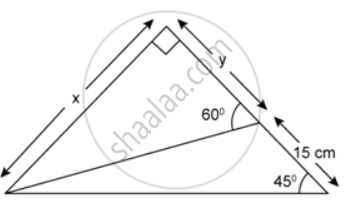
Evaluate the following: `(sin36°)/(cos54°) + (sec31°)/("cosec"59°)`
Evaluate the following: `(3sin^2 40°)/(4cos^2 50°) - ("cosec"^2 28°)/(4sec^2 62°) + (cos10° cos25° cos45° "cosec"80°)/(2sin15° sin25° sin45° sin65° sec75°)`
If sec2θ = cosec3θ, find the value of θ if it is known that both 2θ and 3θ are acute angles.
