Advertisements
Advertisements
Question
If A = B = 60°, verify that: sin(A - B) = sinA cosB - cosA sinB
Solution
sin(A - B) = sinA cosB - cosA sinB
L.H.S. :
sin(A - B) = sin(60°- 60°) = sin0° = 0
R.H.S. :
sinA cosB - cosA sinB
= sin60° cos60° - cos60° sin60°
= `sqrt(3)/(2) xx (1)/(2) - (1)/(2) xx sqrt(3)/(2)`
= `sqrt(3)/(4) - sqrt(3)/(4)`
= 0
L.H.S = R.H.S.
Therefore,
sin(A - B) = sinA cosB - cosA sinB.
APPEARS IN
RELATED QUESTIONS
If 4 sin2 θ - 1= 0 and angle θ is less than 90°, find the value of θ and hence the value of cos2 θ + tan2θ.
Find the magnitude of angle A, if 2 sin A cos A - cos A - 2 sin A + 1 = 0
Find the magnitude of angle A, if tan A - 2 cos A tan A + 2 cos A - 1 = 0
Find the magnitude of angle A, if 2 tan 3A cos 3A - tan 3A + 1 = 2 cos 3A
Solve for 'θ': `sec(θ/2 + 10°) = (2)/sqrt(3)`
In a right triangle ABC, right angled at C, if ∠B = 60° and AB = 15units, find the remaining angles and sides.
Find the length of EC.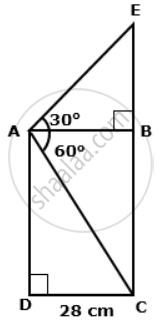
Evaluate the following: `(5sec68°)/("cosec"22°) + (3sin52° sec38°)/(cot51° cot39°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos72° - cos88°
Evaluate the following: sin35° sin45° sec55° sec45°
