Advertisements
Advertisements
Question
If θ = 15°, find the value of: cos3θ - sin6θ + 3sin(5θ + 15°) - 2 tan23θ
Solution
θ = 15°
`(3)/(2)cos3θ - sin6θ + 3sin(5θ + 15°) - 2tan^2 3θ`
= `(3)/(2)cos 3 xx 15° - sin6 xx 15° + 3sin(5 xx 15° + 15°) -2tan^2 3 xx 15°`
= `(3)/(2)cos45° - sin90° + 3sin90° - 2tan^2 45°`
= `(3)/(2) xx (1)/sqrt(2) - 1 + 3 xx 1 - 2 xx (1)^2`
= `(3)/(2sqrt(2)) - 1 + 3 - 2`
= `(3)/(2sqrt(2))`
= `(3)/(2sqrt(2)) xx sqrt(2)/sqrt(2)`
= `(3sqrt(2))/(4)`.
APPEARS IN
RELATED QUESTIONS
If sin x + cos y = 1 and x = 30°, find the value of y
If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.
Find the magnitude of angle A, if 2 cos2 A - 3 cos A + 1 = 0
Find the value of 'A', if 2 sin 2A = 1
Find the length of AD. Given: ∠ABC = 60°, ∠DBC = 45° and BC = 24 cm.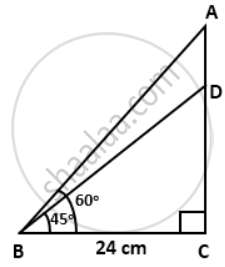
A ladder is placed against a vertical tower. If the ladder makes an angle of 30° with the ground and reaches upto a height of 18 m of the tower; find length of the ladder.
Evaluate the following: cot27° - tan63°
If tan4θ = cot(θ + 20°), find the value of θ if 4θ is an acute angle.
If A, B and C are interior angles of ΔABC, prove that sin`(("A" + "B")/2) = cos "C"/(2)`
Prove the following: sin58° sec32° + cos58° cosec32° = 2
