Advertisements
Advertisements
Question
Prove the following: sin58° sec32° + cos58° cosec32° = 2
Solution
L.H.S.
= sin58° sec32° + cos58° cosec32°
= `sin(90° - 32°) xx (1)/(cos32°) + cos(90° - 32°) xx (1)/(sin32°)`
= `cos32° xx (1)/(cos32°) + sin32° xx (1)/(sin32°)`
= 1 + 1
= 2
= R.H.S.
APPEARS IN
RELATED QUESTIONS
Solve the following equation for A, if 2 sin 3 A = 1
Calculate the value of A, if (tan A - 1) (cosec 3A - 1) = 0
If θ = 15°, find the value of: cos3θ - sin6θ + 3sin(5θ + 15°) - 2 tan23θ
If A = B = 60°, verify that: tan(A - B) = `(tan"A" - tan"B")/(1 + tan"A" tan"B"")`
If `sqrt(3)` sec 2θ = 2 and θ< 90°, find the value of
cos2 (30° + θ) + sin2 (45° - θ)
Find the value of 'y' if `sqrt(3)` = 1.723.
Given your answer correct to 2 decimal places.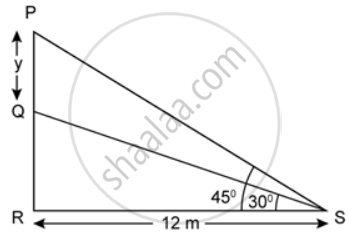
Evaluate the following: `(tan42°)/(cot48°) + (cos33°)/(sin57°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos72° - cos88°
Evaluate the following: `(2sin25° sin35° sec55° sec65°)/(5tan 29° tan45° tan61°) + (3cos20° cos50° cot70° cot40°)/(5tan20° tan50° sin70° sin40°)`
Prove the following: tanθ tan(90° - θ) = cotθ cot(90° - θ)
