Advertisements
Advertisements
Question
If `sqrt(3)` sec 2θ = 2 and θ< 90°, find the value of
cos2 (30° + θ) + sin2 (45° - θ)
Solution
`sqrt(3)`sec 2θ = 2
⇒ sec2θ = `(2)/sqrt(3)`
⇒ sec2θ = sec30°
⇒ 2θ = 30°
⇒ θ =15°
∴ cos2(30° + θ) + sin2(45° - θ)
= cos2(30° + 15°) + sin245° - 15°)
= cos245° sin230°
= `(1/sqrt(2))^2 + (1/2)^2`
= `(1)/(2) + (1)/(4)`
= `(3)/(4)`.
APPEARS IN
RELATED QUESTIONS
If 4 sin2 θ - 1= 0 and angle θ is less than 90°, find the value of θ and hence the value of cos2 θ + tan2θ.
Calculate the value of A, if (cosec 2A - 2) (cot 3A - 1) = 0
Solve for x : sin2 x + sin2 30° = 1
Solve for x : sin2 60° + cos2 (3x- 9°) = 1
In the given figure, PQ = 6 cm, RQ = x cm and RP = 10 cm, find
a. cosθ
b. sin2θ- cos2θ
c. Use tanθ to find the value of RQ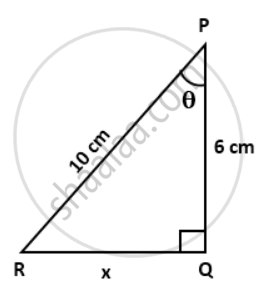
Find the value of 'x' in each of the following: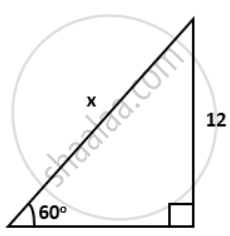
Find lengths of diagonals AC and BD. Given AB = 24 cm and ∠BAD = 60°.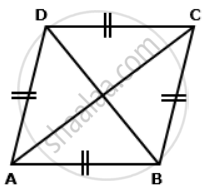
In the given figure, ∠B = 60°, ∠C = 30°, AB = 8 cm and BC = 24 cm. Find:
a. BE
b. AC
Evaluate the following: `(sec34°)/("cosec"56°)`
Evaluate the following: `(5sec68°)/("cosec"22°) + (3sin52° sec38°)/(cot51° cot39°)`
