Advertisements
Advertisements
प्रश्न
If `sqrt(3)` sec 2θ = 2 and θ< 90°, find the value of
cos2 (30° + θ) + sin2 (45° - θ)
उत्तर
`sqrt(3)`sec 2θ = 2
⇒ sec2θ = `(2)/sqrt(3)`
⇒ sec2θ = sec30°
⇒ 2θ = 30°
⇒ θ =15°
∴ cos2(30° + θ) + sin2(45° - θ)
= cos2(30° + 15°) + sin245° - 15°)
= cos245° sin230°
= `(1/sqrt(2))^2 + (1/2)^2`
= `(1)/(2) + (1)/(4)`
= `(3)/(4)`.
APPEARS IN
संबंधित प्रश्न
State for any acute angle θ whether sin θ increases or decreases as θ increases
Solve the following equation for A, if 2cos2A = 1
Solve for x : cos `(x/(2)+10°) = (sqrt3)/(2)`
Find the value of 'A', if `sqrt(3)cot"A"` = 1
If A = 30°, verify that cos2θ = `(1 - tan^2 θ)/(1 + tan^2 θ)` = cos4θ - sin4θ = 2cos2θ - 1 - 2sin2θ
In a trapezium ABCD, as shown, AB ‖ DC, AD = DC = BC = 24 cm and ∠A = 30°. Find: length of AB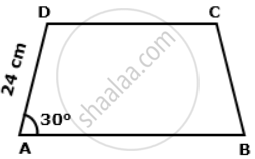
Evaluate the following: `(cos34° cos35°)/(sin57° sin56°)`
Evaluate the following: sin(35° + θ) - cos(55° - θ) - tan(42° + θ) + cot(48° - θ)
If cos3θ = sin(θ - 34°), find the value of θ if 3θ is an acute angle.
If secθ= cosec30° and θ is an acute angle, find the value of 4 sin2θ - 2 cos2θ.
