Advertisements
Advertisements
प्रश्न
In a trapezium ABCD, as shown, AB ‖ DC, AD = DC = BC = 24 cm and ∠A = 30°. Find: length of AB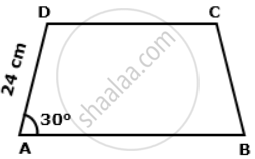
उत्तर
Construction: Draw DP ⊥ AB and CM ⊥ AB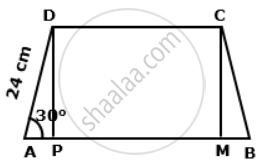
a. In right ΔADP,
cos30° = `"AP"/"AD"`
⇒ `sqrt(3)/(2) = "AP"/(24)`
⇒ AP = `12sqrt(13)"cm"`
Similarly, from right ΔBCM, we have MB = `12sqrt(3)"cm"`
Now, in rectangle PMCD, we have CD = PM = 24cm
∴ Length of AB
= AP + PM + MB
= `12sqrt(3) + 24 + 12sqrt(3)`
= `24(sqrt(3) + 1)"cm"`.
b. In right ΔADP,
sin30° = `"PD"/"AD"`
⇒ `(1)/(2) = "PD"/(24)`
⇒ PD = 12cm
Similarly, from right ΔBCM, we have MB = `12sqrt(3)"cm"`
Now, in rectangle PMCD, we have CD = PM = 24cm
∴ Length of AB
= AP + PM + MB
= `12sqrt(3) + 24 + 12sqrt(3)`
= `24(sqrt(3) + 1)"cm"`.
APPEARS IN
संबंधित प्रश्न
Calculate the value of A, if (sec 2A - 1) (cosec 3A - 1) = 0
Find the magnitude of angle A, if 2 tan 3A cos 3A - tan 3A + 1 = 2 cos 3A
Solve for x : 2 cos (3x - 15°) = 1
If θ = 30°, verify that: sin 3θ = 4sinθ . sin(60° - θ) sin(60° + θ)
If A = B = 60°, verify that: sin(A - B) = sinA cosB - cosA sinB
Find the length of AD. Given: ∠ABC = 60°, ∠DBC = 45° and BC = 24 cm.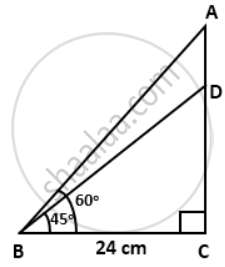
Find the value of 'y' if `sqrt(3)` = 1.723.
Given your answer correct to 2 decimal places.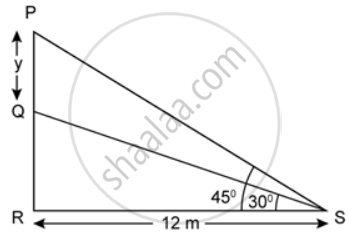
Evaluate the following: `(cos34° cos35°)/(sin57° sin56°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos72° - cos88°
Evaluate the following: `(5cot5° cot15° cot25° cot35° cot45°)/(7tan45° tan55° tan65° tan75° tan85°) + (2"cosec"12° "cosec"24° cos78° cos66°)/(7sin14° sin23° sec76° sec67°)`
