Advertisements
Advertisements
प्रश्न
Find lengths of diagonals AC and BD. Given AB = 24 cm and ∠BAD = 60°.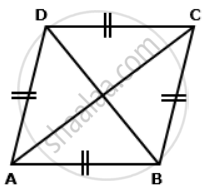
उत्तर

The given figure is a rhombus as all sides are equal. we know that diagonals of a rhombus bisect each other at right angles and also bisect the angle of vertex.
Let the diagonals AC and BD intersect each other at O.
⇒ OA = `"OC" - (1)/(2)"AC", "OB" = "OD" = (1)/(2)"BD"`, ∠AOB = 90°
Now, ∠BAD = 60°
⇒ ∠OAB = `(1)/(2)∠"BAD"` = 30°
In right-angled AOB,
sin30° = `"OB"/"AB"`
⇒ `(1)/(2) = "OB"/(24)`
⇒ OB = 12cm
cos30° = `"OA"/"AB"`
⇒ `sqrt(3)/(2) = "OA"/(24)`
⇒ OA = `12sqrt(3)"cm"`
∴ Length of diagonal AC
= 2 x OA
= `2 xx 2sqrt(3)`
= `24sqrt(3)"cm"`
And, length of diagonal BD
= 2 x OB
= 2 x 12
= 24cm.
APPEARS IN
संबंधित प्रश्न
Solve the following equation for A, if 2 sin 3 A = 1
Solve for x : cos (2x - 30°) = 0
Solve for x : cos2 30° + cos2 x = 1
Evaluate the following: `((sin3θ - 2sin4θ))/((cos3θ - 2cos4θ))` when 2θ = 30°
If A = B = 60°, verify that: cos(A - B) = cosA cosB + sinA sinB
If θ < 90°, find the value of: `tan^2θ - (1)/cos^2θ`
Evaluate the following: sin22° cos44° - sin46° cos68°
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos84° + cosec69° - cot68°
Evaluate the following: `(3sin^2 40°)/(4cos^2 50°) - ("cosec"^2 28°)/(4sec^2 62°) + (cos10° cos25° cos45° "cosec"80°)/(2sin15° sin25° sin45° sin65° sec75°)`
Prove the following: `(tan(90° - θ)cotθ)/("cosec"^2 θ)` = cos2θ
