Advertisements
Advertisements
प्रश्न
Find the length of AD. Given: ∠ABC = 60°, ∠DBC = 45° and BC = 24 cm.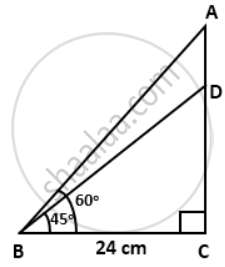
उत्तर

In ΔABC,
tan60° = `"AC"/"BC"`
⇒ `sqrt(3) = "AC"/(24)`
⇒ AC = `24sqrt(3)"cm"`
In ΔDBC,
tan45° = `"DC"/"BC"`
⇒ 1 = `"DC"/(24)`
⇒ DC = 24cm
Now,
AC = AD + DC
⇒ AD
= AC - DC
= `24sqrt(3) - 24`
= `24(sqrt(3) - 1)"cm"`.
APPEARS IN
संबंधित प्रश्न
Find the magnitude of angle A, if 2 cos2 A - 3 cos A + 1 = 0
Solve for x : sin (x + 10°) = `(1)/(2)`
Solve for x : tan2 (x - 5°) = 3
Evaluate the following: `((1 - cosθ)(1 + cosθ))/((1 - sinθ)(1 + sinθ)` if θ = 30°
If θ = 15°, find the value of: cos3θ - sin6θ + 3sin(5θ + 15°) - 2 tan23θ
If A = B = 60°, verify that: sin(A - B) = sinA cosB - cosA sinB
If `sqrt(3)` sec 2θ = 2 and θ< 90°, find the value of
cos2 (30° + θ) + sin2 (45° - θ)
Evaluate the following: cosec 54° - sec 36°
Evaluate the following: tan(78° + θ) + cosec(42° + θ) - cot(12° - θ) - sec(48° - θ)
If A, B and C are interior angles of ΔABC, prove that sin`(("A" + "B")/2) = cos "C"/(2)`
