Advertisements
Advertisements
प्रश्न
Evaluate the following: `(3sin^2 40°)/(4cos^2 50°) - ("cosec"^2 28°)/(4sec^2 62°) + (cos10° cos25° cos45° "cosec"80°)/(2sin15° sin25° sin45° sin65° sec75°)`
उत्तर
`(3sin^2 40°)/(4cos^2 50°) - ("cosec"^2 28°)/(4sec^2 62°) + (cos10° cos25° cos45° "cosec"80°)/(2sin15° sin25° sin45° sin65° sec75°)`
= `(3sin^2 (90° - 50°))/(4cos^2 50°) - ("cosec"^2 (90° - 62°))/(4sec^2 62°) + (cos(90° - 80°) cos25° xx 1/sqrt(2) xx 1/(sin80°))/(2sin(90° - 75°) xx 1/sqrt(2) xx sin(90° - 25°) xx 1/(cos75°))`
= `(3cos^2 50°)/(4cos^2 50°) - (sec^2 62°)/(4sec^2 62°) + (sin80° xx cos25° xx 1/(cos75°))/(2cos75° xx cos25° xx 1/(cos75°))`
= `(3)/(4) - (1)/(4) + (1)/(2)`
= `(1)/(2) + (1)/(2)`
= 1.
APPEARS IN
संबंधित प्रश्न
State for any acute angle θ whether tan θ increases or decreases as θ decreases.
If sin 3A = 1 and 0 < A < 90°, find `tan^2A - (1)/(cos^2 "A")`
If 3 tan A - 5 cos B = `sqrt3` and B = 90°, find the value of A
Solve for 'θ': cot2(θ - 5)° = 3
If θ = 30°, verify that: 1 - sin 2θ = (sinθ - cosθ)2
If A = B = 60°, verify that: sin(A - B) = sinA cosB - cosA sinB
In a right triangle ABC, right angled at C, if ∠B = 60° and AB = 15units, find the remaining angles and sides.
Find the value 'x', if: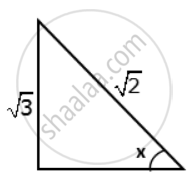
A ladder is placed against a vertical tower. If the ladder makes an angle of 30° with the ground and reaches upto a height of 18 m of the tower; find length of the ladder.
The perimeter of a rhombus is 100 cm and obtuse angle of it is 120°. Find the lengths of its diagonals.
