Advertisements
Advertisements
प्रश्न
Evaluate the following: `(3sin^2 40°)/(4cos^2 50°) - ("cosec"^2 28°)/(4sec^2 62°) + (cos10° cos25° cos45° "cosec"80°)/(2sin15° sin25° sin45° sin65° sec75°)`
उत्तर
`(3sin^2 40°)/(4cos^2 50°) - ("cosec"^2 28°)/(4sec^2 62°) + (cos10° cos25° cos45° "cosec"80°)/(2sin15° sin25° sin45° sin65° sec75°)`
= `(3sin^2 (90° - 50°))/(4cos^2 50°) - ("cosec"^2 (90° - 62°))/(4sec^2 62°) + (cos(90° - 80°) cos25° xx 1/sqrt(2) xx 1/(sin80°))/(2sin(90° - 75°) xx 1/sqrt(2) xx sin(90° - 25°) xx 1/(cos75°))`
= `(3cos^2 50°)/(4cos^2 50°) - (sec^2 62°)/(4sec^2 62°) + (sin80° xx cos25° xx 1/(cos75°))/(2cos75° xx cos25° xx 1/(cos75°))`
= `(3)/(4) - (1)/(4) + (1)/(2)`
= `(1)/(2) + (1)/(2)`
= 1.
APPEARS IN
संबंधित प्रश्न
State for any acute angle θ whether sin θ increases or decreases as θ increases
State for any acute angle θ whether cos θ increases or decreases as θ increases.
Find the magnitude of angle A, if tan A - 2 cos A tan A + 2 cos A - 1 = 0
Find the value of 'A', if 2 cos A = 1
Find lengths of diagonals AC and BD. Given AB = 24 cm and ∠BAD = 60°.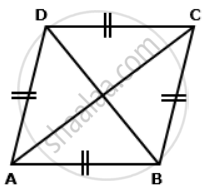
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:
a. AB
b. AC
c. AE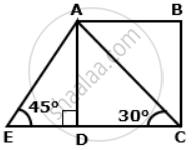
Find:
a. BC
b. AD
c. AC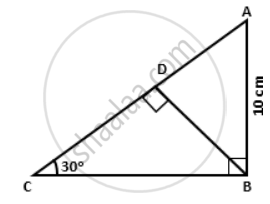
Find the value 'x', if: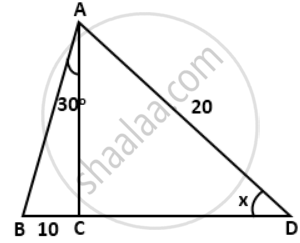
In the given figure, if tan θ = `(5)/(13), tan α = (3)/(5)` and RS = 12m, find the value of 'h'.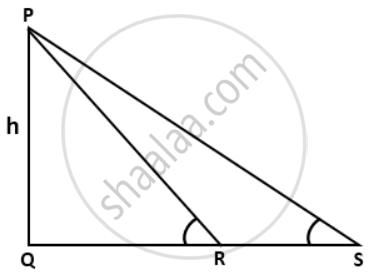
Evaluate the following: `(sin25° cos43°)/(sin47° cos 65°)`
