Advertisements
Advertisements
प्रश्न
Find lengths of diagonals AC and BD. Given AB = 24 cm and ∠BAD = 60°.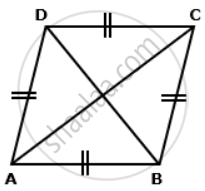
उत्तर

The given figure is a rhombus as all sides are equal. we know that diagonals of a rhombus bisect each other at right angles and also bisect the angle of vertex.
Let the diagonals AC and BD intersect each other at O.
⇒ OA = `"OC" - (1)/(2)"AC", "OB" = "OD" = (1)/(2)"BD"`, ∠AOB = 90°
Now, ∠BAD = 60°
⇒ ∠OAB = `(1)/(2)∠"BAD"` = 30°
In right-angled AOB,
sin30° = `"OB"/"AB"`
⇒ `(1)/(2) = "OB"/(24)`
⇒ OB = 12cm
cos30° = `"OA"/"AB"`
⇒ `sqrt(3)/(2) = "OA"/(24)`
⇒ OA = `12sqrt(3)"cm"`
∴ Length of diagonal AC
= 2 x OA
= `2 xx 2sqrt(3)`
= `24sqrt(3)"cm"`
And, length of diagonal BD
= 2 x OB
= 2 x 12
= 24cm.
APPEARS IN
संबंधित प्रश्न
Solve the following equation for A, if sin 3 A = `sqrt3 /2`
If sin 3A = 1 and 0 < A < 90°, find sin A
Calculate the value of A, if (cosec 2A - 2) (cot 3A - 1) = 0
If sin 3A = 1 and 0 < A < 90°, find `tan^2A - (1)/(cos^2 "A")`
Solve for x : cos `(x/(2)+10°) = (sqrt3)/(2)`
If ΔABC is a right triangle such that ∠C = 90°, ∠A = 45° and BC =7units, find ∠B, AB and AC.
Find the value of 'x' in each of the following: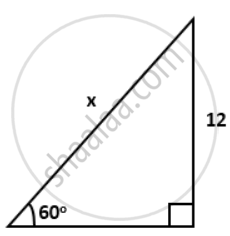
Find the value of 'y' if `sqrt(3)` = 1.723.
Given your answer correct to 2 decimal places.
In right-angled triangle ABC; ∠B = 90°. Find the magnitude of angle A, if:
a. AB is `sqrt(3)` times of BC.
B. BC is `sqrt(3)` times of BC.
Evaluate the following: cosec 54° - sec 36°
