Advertisements
Advertisements
प्रश्न
Calculate the value of A, if (cosec 2A - 2) (cot 3A - 1) = 0
उत्तर
( cosec 2A – 2) (cot 3A – 1) = 0
cosec 2A – 2 = 0 and cot 3A – 1 = 0
cosec 2A = 2 and cot 3A = 1
cosec 2A = cosec 30° and cot 3A = cot 45°
2A = 30° and 3A = 45°
A = 15° and A = 15°
APPEARS IN
संबंधित प्रश्न
If sin x + cos y = 1 and x = 30°, find the value of y
If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.
Find the value of 'A', if `sqrt(3)cot"A"` = 1
If θ = 15°, find the value of: cos3θ - sin6θ + 3sin(5θ + 15°) - 2 tan23θ
If A = B = 60°, verify that: tan(A - B) = `(tan"A" - tan"B")/(1 + tan"A" tan"B"")`
Find the value 'x', if: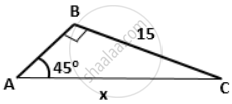
Evaluate the following: `(tan42°)/(cot48°) + (cos33°)/(sin57°)`
Evaluate the following: cos39° cos48° cos60° cosec42° cosec51°
If cos3θ = sin(θ - 34°), find the value of θ if 3θ is an acute angle.
Prove the following: sin58° sec32° + cos58° cosec32° = 2
