Advertisements
Advertisements
प्रश्न
If A = B = 60°, verify that: tan(A - B) = `(tan"A" - tan"B")/(1 + tan"A" tan"B"")`
उत्तर
tan(A - B) = `(tan"A" - tan"B")/(1 + tan"A" tan"B"")`
L.H.S. :
tan(A - B) = tan(60° - 60°) - tan0° = 0
R.H.S. :
`(tan"A" - tan"B")/(1 + tan"A" tan"B"")`
= `(tan 60° - tan60°)/(1 + tan60° tan60°)`
= `(sqrt(3) - sqrt(3))/(1 + sqrt(3) xx sqrt(3)`
= 0
L.H.S = R.H.S.
Therefore,
tan(A - B) = `(tan"A" - tan"B")/(1 + tan"A" tan"B"")`.
APPEARS IN
संबंधित प्रश्न
Solve the following equation for A, if sin 3 A = `sqrt3 /2`
If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.
If sin 3A = 1 and 0 < A < 90°, find cos 2A
Find the magnitude of angle A, if tan A - 2 cos A tan A + 2 cos A - 1 = 0
If θ = 30°, verify that: tan2θ = `(2tanθ)/(1 - tan^2θ)`
In a rectangle ABCD, AB = 20cm, ∠BAC = 60°, calculate side BC and diagonals AC and BD.
Find the value 'x', if: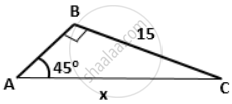
Evaluate the following: `(cos34° cos35°)/(sin57° sin56°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos72° - cos88°
Prove the following: sin58° sec32° + cos58° cosec32° = 2
