Advertisements
Advertisements
प्रश्न
In a right triangle ABC, right angled at C, if ∠B = 60° and AB = 15units, find the remaining angles and sides.
उत्तर
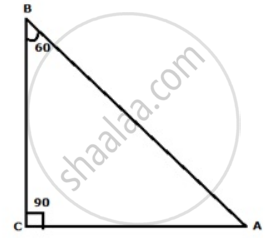
∠B = 60°
∠C = 90° ...(Since triangle ABC is right angled at C)
∠A + ∠B + ∠C = 180°
∠A + 60° + 90° =180°
∠A = 180° - 150°
∠A = 30°
Now,
sin60° = `"AC"/"AB"`
AC = sin60° x AB
AC = `sqrt(3)/(2) xx 15`
AC = `(15sqrt(3))/(2)"units"`
Also,
cos60° = `"BC"/"AB"`
BC = cos60° x AB
BC = `(1)/(2) xx 15`
BC = 7.5units.
APPEARS IN
संबंधित प्रश्न
If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.
If sin α + cosβ = 1 and α= 90°, find the value of 'β'.
If A = 30°, verify that cos2θ = `(1 - tan^2 θ)/(1 + tan^2 θ)` = cos4θ - sin4θ = 2cos2θ - 1 - 2sin2θ
Find the value of 'y' if `sqrt(3)` = 1.723.
Given your answer correct to 2 decimal places.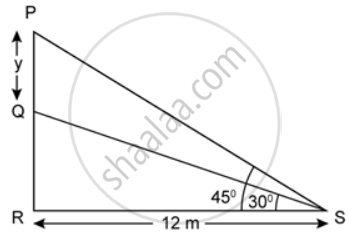
Evaluate the following: `(sin36°)/(cos54°) + (sec31°)/("cosec"59°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: sin65° + cot59°
Evaluate the following: cos39° cos48° cos60° cosec42° cosec51°
Evaluate the following: `(3sin37°)/(cos53°) - (5"cosec"39°)/(sec51°) + (4tan23° tan37° tan67° tan53°)/(cos17° cos67° "cosec"73° "cosec"23°)`
If tan4θ = cot(θ + 20°), find the value of θ if 4θ is an acute angle.
Prove the following: sin58° sec32° + cos58° cosec32° = 2
