Advertisements
Advertisements
प्रश्न
If A = B = 60°, verify that: cos(A - B) = cosA cosB + sinA sinB
उत्तर
cos(A - B) = cosA cosB + sinA sinB
L.H.S. :
cos(60° - 60°) = cos0° = 1
R.H.S. :
cosA cosB + sinA sinB
= cos60° cos60° + sin60° sin60°
= `(1)/(2) xx (1)/(2) + sqrt(3)/(2) xx sqrt(3)/(2)`
= `(1)/(4) + (3)/(4)`
= `(4)/(4)`
= 1
L.H.S. = R.H.S.
Therefore,
cos(A - B) = cosA cosB + sinA sinB.
APPEARS IN
संबंधित प्रश्न
From the given figure,
find:
(i) cos x°
(ii) x°
(iii) `(1)/(tan^2 xx°) – (1)/(sin^2xx°)`
(iv) Use tan xo, to find the value of y.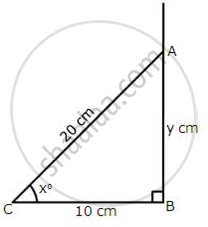
Solve for x : 2 cos (3x - 15°) = 1
Find the value of 'A', if (1 - cosec A)(2 - sec A) = 0
Evaluate the following: `((sin3θ - 2sin4θ))/((cos3θ - 2cos4θ))` when 2θ = 30°
If `sqrt(3)`sec 2θ = 2 and θ< 90°, find the value of θ
Find the value of 'x' in each of the following: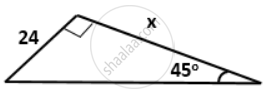
In the given figure; ∠B = 90°, ∠ADB = 30°, ∠ACB = 45° and AB = 24 m. Find the length of CD.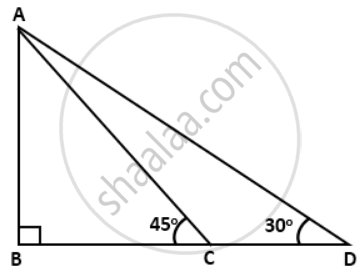
If A, B and C are interior angles of ΔABC, prove that sin`(("A" + "B")/2) = cos "C"/(2)`
Prove the following: sin58° sec32° + cos58° cosec32° = 2
If A + B = 90°, prove that `(tan"A" tan"B" + tan"A" cot"B")/(sin"A" sec"B") - (sin^2"B")/(cos^2"A")` = tan2A
