Advertisements
Advertisements
प्रश्न
If secθ= cosec30° and θ is an acute angle, find the value of 4 sin2θ - 2 cos2θ.
उत्तर
secθ= cosec30°
⇒ secθ = 2
⇒ secθ = sec60°
⇒ θ = 60°
Now,
4sin2θ - 2cos2θ
= 4sin260° - 2cos260°
=
=
=
=
=
APPEARS IN
संबंधित प्रश्न
Use the given figure to find:
(i) tan θ°
(ii) θ°
(iii) sin2θ° - cos2θ°
(iv) Use sin θ° to find the value of x.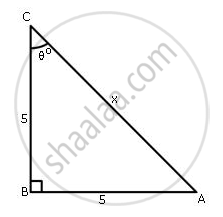
Find the magnitude of angle A, if 2 sin A cos A - cos A - 2 sin A + 1 = 0
In ΔABC, ∠B = 90° , AB = y units, BC =
- sin x°
- x°
- tan x°
- use cos x° to find the value of y.
If sin 3A = 1 and 0 < A < 90°, find cos 2A
Solve for x : cos2 30° + cos2 x = 1
Find x and y, in each of the following figure: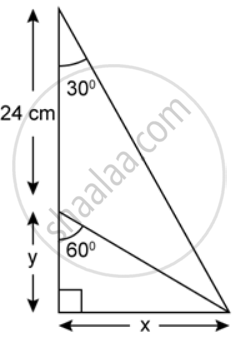
A ladder is placed against a vertical tower. If the ladder makes an angle of 30° with the ground and reaches upto a height of 18 m of the tower; find length of the ladder.
If sec2θ = cosec3θ, find the value of θ if it is known that both 2θ and 3θ are acute angles.
If P, Q and R are the interior angles of ΔPQR, prove that
If A + B = 90°, prove that
