Advertisements
Advertisements
प्रश्न
If 4 sin2 θ - 1= 0 and angle θ is less than 90°, find the value of θ and hence the value of cos2 θ + tan2θ.
उत्तर
4 sin2 θ – 1 = 0
sin2 θ = `(1)/(4)`
sin θ = `(1)/(2)`
sin θ = sin30°
θ = 30°
cos2 θ + tan2 θ= cos230° + tan230°
= `(sqrt3/2)^2 + ( 1/sqrt3)^2`
= `(3)/(4) + (1)/(3)`
= `(9 + 4)/(12)`
= `(13)/(12)`
APPEARS IN
संबंधित प्रश्न
Solve the following equations for A, if `sqrt3` tan A = 1
Solve for x : tan2 (x - 5°) = 3
Find the value of 'A', if 2cos 3A = 1
If A = 30°, verify that cos2θ = `(1 - tan^2 θ)/(1 + tan^2 θ)` = cos4θ - sin4θ = 2cos2θ - 1 - 2sin2θ
Evaluate the following: `((sin3θ - 2sin4θ))/((cos3θ - 2cos4θ))` when 2θ = 30°
If θ = 15°, find the value of: cos3θ - sin6θ + 3sin(5θ + 15°) - 2 tan23θ
In the given figure, PQ = 6 cm, RQ = x cm and RP = 10 cm, find
a. cosθ
b. sin2θ- cos2θ
c. Use tanθ to find the value of RQ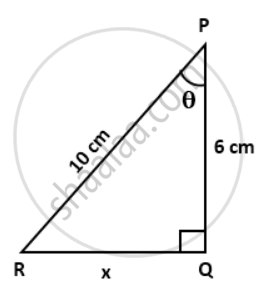
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: sin53° + sec66° - sin50°
Evaluate the following: `(sin0° sin35° sin55° sin75°)/(cos22° cos64° cos58° cos90°)`
Evaluate the following: `(2sin25° sin35° sec55° sec65°)/(5tan 29° tan45° tan61°) + (3cos20° cos50° cot70° cot40°)/(5tan20° tan50° sin70° sin40°)`
