Advertisements
Advertisements
Question
State for any acute angle θ whether tan θ increases or decreases as θ decreases.
Options
Increases
Decreases
Solution
For acute angles, remember what tangent means: opposite over base. If we decrease the angle, then the opposite side gets smaller. That means "opposite /base" decreases.
APPEARS IN
RELATED QUESTIONS
In ΔABC, ∠B = 90° , AB = y units, BC = `(sqrt3)` units, AC = 2 units and angle A = x°, find:
- sin x°
- x°
- tan x°
- use cos x° to find the value of y.
If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.
Solve for x : 2 cos (3x - 15°) = 1
Solve for x : sin2 60° + cos2 (3x- 9°) = 1
Find the value of 'A', if 2cos 3A = 1
In a trapezium ABCD, as shown, AB ‖ DC, AD = DC = BC = 24 cm and ∠A = 30°. Find: length of AB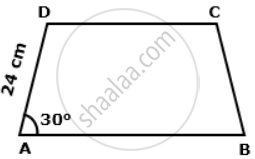
Find the value 'x', if:
Evaluate the following: sin22° cos44° - sin46° cos68°
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: tan77° - cot63° + sin57°
Evaluate the following: sin(35° + θ) - cos(55° - θ) - tan(42° + θ) + cot(48° - θ)
