Advertisements
Advertisements
Question
State for any acute angle θ whether cos θ increases or decreases as θ increases.
Options
Increases
Decreases
Solution
Increases
Explanation:
For acute angles, remember what cosine means: base over hypotenuse. If we increase the angle, then the hypotenuse side gets larger. That means "base/hypotenuse" gets smaller or decreases.
APPEARS IN
RELATED QUESTIONS
If 4 cos2 x° - 1 = 0 and 0 ∠ x° ∠ 90°,
find:(i) x°
(ii) sin2 x° + cos2 x°
(iii) `(1)/(cos^2xx°) – (tan^2 xx°)`
Solve for x : sin2 x + sin2 30° = 1
Find the value of 'A', if cosec 3A = `(2)/sqrt(3)`
Find the value of 'x' in each of the following:
Find the value 'x', if: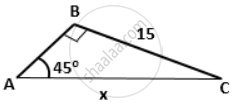
Evaluate the following: cot27° - tan63°
Evaluate the following: `(sin36°)/(cos54°) + (sec31°)/("cosec"59°)`
Evaluate the following: `(2sin28°)/(cos62°) + (3cot49°)/(tan41°)`
If tan4θ = cot(θ + 20°), find the value of θ if 4θ is an acute angle.
If sec2θ = cosec3θ, find the value of θ if it is known that both 2θ and 3θ are acute angles.
