Advertisements
Advertisements
Question
From the given figure,
find:
(i) cos x°
(ii) x°
(iii) `(1)/(tan^2 xx°) – (1)/(sin^2xx°)`
(iv) Use tan xo, to find the value of y.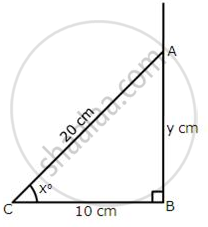
Solution
(i) cos x° = `(10)/(20)`
cos x° = `(1)/(2)`
(ii) cos x° = `(1)/(2)`
cos x° = cos 60°
x° = 60°
(iii) `(1)/(tan^2x°) – (1)/(sin^2x°) = (1)/(tan^2 60°) – (1)/(sin^2 60°)`
= `(1)/(sqrt3)^2 – (1)/(sqrt3/2)^2`
= `(1)/(3) – (4)/(3)`
= – 1
(iv) tan x° = tan 60°
= `sqrt3`
We know that tan x° = `"AB"/"BC"`
⇒ tan x° = `"y"/(10)`
⇒ y = 10 tan x°
⇒ y = 10 tan 60°
⇒ y = 10`sqrt3`
APPEARS IN
RELATED QUESTIONS
Calculate the value of A, if (sin A - 1) (2 cos A - 1) = 0
Solve the following equations for A, if `sqrt3` tan A = 1
Find the value of 'A', if 2cos 3A = 1
If `sqrt(2) = 1.414 and sqrt(3) = 1.732`, find the value of the following correct to two decimal places tan60°
In a rectangle ABCD, AB = 20cm, ∠BAC = 60°, calculate side BC and diagonals AC and BD.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:
a. AB
b. AC
c. AE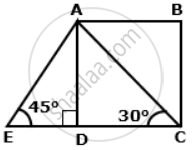
In the given figure, a rocket is fired vertically upwards from its launching pad P. It first rises 20 km vertically upwards and then 20 km at 60° to the vertical. PQ represents the first stage of the journey and QR the second. S is a point vertically below R on the horizontal level as P, find:
a. the height of the rocket when it is at point R.
b. the horizontal distance of point S from P.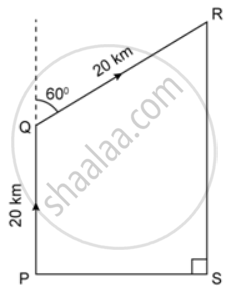
Evaluate the following: `(sec34°)/("cosec"56°)`
Evaluate the following: cosec 54° - sec 36°
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cosec64° + sec70°
