Advertisements
Advertisements
Question
If sin 3A = 1 and 0 < A < 90°, find `tan^2A - (1)/(cos^2 "A")`
Sum
Solution
sin 3A = 1
sin 3A = sin90°
3A = 90°
A = 30°
`tan^2A – (1)/(cos^2"A") = tan^2 30° – (1)/(cos^2 30°)`
= `(1/sqrt3)^2 – (1)/(sqrt3/2)^2`
= `(1)/(3) – (4)/(3)`
= `(–3)/(3)`
= – 1
shaalaa.com
Trigonometric Equation Problem and Solution
Is there an error in this question or solution?
APPEARS IN
RELATED QUESTIONS
If 4 cos2 x° - 1 = 0 and 0 ∠ x° ∠ 90°,
find:(i) x°
(ii) sin2 x° + cos2 x°
(iii) `(1)/(cos^2xx°) – (tan^2 xx°)`
Solve for x : 2 cos 3x - 1 = 0
Solve for x : cos `(x)/(3) –1` = 0
If A = B = 60°, verify that: cos(A - B) = cosA cosB + sinA sinB
Find the value of 'x' in each of the following: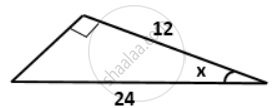
Find the value 'x', if: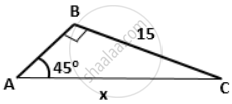
Find the value 'x', if: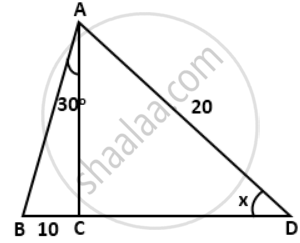
Evaluate the following: sin31° - cos59°
Evaluate the following: `(2sin28°)/(cos62°) + (3cot49°)/(tan41°)`
Evaluate the following: tan(78° + θ) + cosec(42° + θ) - cot(12° - θ) - sec(48° - θ)
