Advertisements
Advertisements
Question
Solve for x : 2 cos 3x - 1 = 0
Solution
2 cos 3x – 1 = 0
cos 3x = `(1)/(2)`
3x = 60°
x = 20°
APPEARS IN
RELATED QUESTIONS
If 2 sin x° - 1 = 0 and x° is an acute angle; find:
- sin x°
- x°
- cos x° and tan x°.
Use the given figure to find:
(i) tan θ°
(ii) θ°
(iii) sin2θ° - cos2θ°
(iv) Use sin θ° to find the value of x.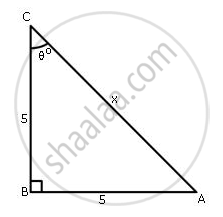
State for any acute angle θ whether cos θ increases or decreases as θ increases.
Find the magnitude of angle A, if 2 tan 3A cos 3A - tan 3A + 1 = 2 cos 3A
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 1.5 cm each and are perpendicular to AB. Given that ∠AED = 45° and ∠ACD = 30°. Find:
a. AB
b. AC
c. AE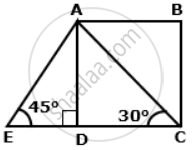
Evaluate the following: `(cos34° cos35°)/(sin57° sin56°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cosec64° + sec70°
Evaluate the following: `(sin0° sin35° sin55° sin75°)/(cos22° cos64° cos58° cos90°)`
Evaluate the following: `(2sin25° sin35° sec55° sec65°)/(5tan 29° tan45° tan61°) + (3cos20° cos50° cot70° cot40°)/(5tan20° tan50° sin70° sin40°)`
If P, Q and R are the interior angles of ΔPQR, prove that `cot(("Q" + "R")/2) = tan "P"/(2)`
