Advertisements
Advertisements
प्रश्न
Evaluate the following: sin(35° + θ) - cos(55° - θ) - tan(42° + θ) + cot(48° - θ)
उत्तर
sin(35° + θ) - cos(55° - θ) - tan(42° + θ) + cot(48° - θ)
= sin[90° - (55° - θ)] - cos(55° - θ) - tan[90° - (48° - θ)] + cot(48° - θ)
= cos(55° - θ) - cos(55° - θ) - cot(48° - θ) + cot(48° - θ)
= 0.
APPEARS IN
संबंधित प्रश्न
State for any acute angle θ whether sin θ increases or decreases as θ increases
In ΔABC, ∠B = 90° , AB = y units, BC = `(sqrt3)` units, AC = 2 units and angle A = x°, find:
- sin x°
- x°
- tan x°
- use cos x° to find the value of y.
State for any acute angle θ whether tan θ increases or decreases as θ decreases.
Solve the following equation for A, if 2 sin A = 1
Find the value of 'A', if `sqrt(3)cot"A"` = 1
Find the value of 'x' in each of the following: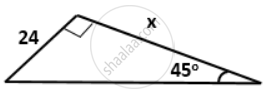
In right-angled triangle ABC; ∠B = 90°. Find the magnitude of angle A, if:
a. AB is `sqrt(3)` times of BC.
B. BC is `sqrt(3)` times of BC.
Evaluate the following: `(sin36°)/(cos54°) + (sec31°)/("cosec"59°)`
If tan4θ = cot(θ + 20°), find the value of θ if 4θ is an acute angle.
Prove the following: sin230° + cos230° = `(1)/(2)sec60°`
