Advertisements
Advertisements
प्रश्न
Evaluate the following: tan(78° + θ) + cosec(42° + θ) - cot(12° - θ) - sec(48° - θ)
उत्तर
tan(78° + θ) + cosec(42° + θ) - cot(12° - θ) - sec(48° - θ)
= tan[90° - (12° - θ)] + cosec[90° - (48° - θ)] - cot(12° - θ) - sec(48° - θ)
= cot(12° - θ) + sec(48° - θ)] - cot(12° - θ) - sec(48° - θ)
= 0.
APPEARS IN
संबंधित प्रश्न
If 4 sin2 θ - 1= 0 and angle θ is less than 90°, find the value of θ and hence the value of cos2 θ + tan2θ.
If sin 3A = 1 and 0 < A < 90°, find sin A
Solve the following equations for A, if `sqrt3` tan A = 1
Solve for x : cos (2x - 30°) = 0
Find the value of 'A', if cosec 3A = `(2)/sqrt(3)`
Find the length of AD. Given: ∠ABC = 60°, ∠DBC = 45° and BC = 24 cm.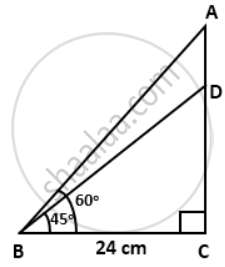
Evaluate the following: `(sec32° cot26°)/(tan64° "cosec"58°)`
Evaluate the following: sin28° sec62° + tan49° tan41°
Evaluate the following: `(sin36°)/(cos54°) + (sec31°)/("cosec"59°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos84° + cosec69° - cot68°
