Advertisements
Advertisements
प्रश्न
If tan x° = `(5)/(12) . tan y° = (3)/(4)` and AB = 48m; find the length CD.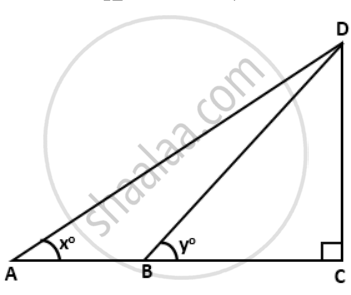
उत्तर

tan x = `"CD"/"AC"`
⇒ `(5)/(12) = "CD"/"AC"`
⇒ 5 x AC = 12 x CD
⇒ 5(AB + BC) = 12CD
⇒ 5(48 + BC) = 12CD
⇒ 48 + BC = `(12"CD")/(5)` ....(i)
tan y = `"CD"/"BC"`
⇒ `(3)/(4) = "CD"/"BC"`
⇒ 3BC = 4CD
⇒ BC = `(6"CD")/(3)` ....(ii)
Substituting (ii) in (i), we have
`48 + (4"CD")/(3) = (12"CD")/(5)`
⇒ `(12"CD")/(5) - (4"CD")/(3)` = 48
⇒ `(36"CD" - 20"CD")/(15)` = 48
⇒ 16CD = 720
⇒ CD = 45m.
APPEARS IN
संबंधित प्रश्न
State for any acute angle θ whether tan θ increases or decreases as θ decreases.
Solve for 'θ': `sec(θ/2 + 10°) = (2)/sqrt(3)`
If A = B = 60°, verify that: cos(A - B) = cosA cosB + sinA sinB
Find the value 'x', if:
Find the value 'x', if: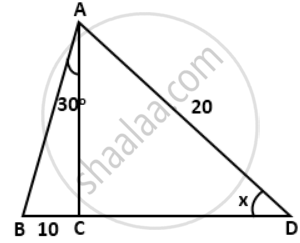
Evaluate the following: `(cos34° cos35°)/(sin57° sin56°)`
Evaluate the following: `(5sec68°)/("cosec"22°) + (3sin52° sec38°)/(cot51° cot39°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: sin65° + cot59°
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: sin53° + sec66° - sin50°
If P, Q and R are the interior angles of ΔPQR, prove that `cot(("Q" + "R")/2) = tan "P"/(2)`
