Advertisements
Advertisements
प्रश्न
In the given figure, PQ = 6 cm, RQ = x cm and RP = 10 cm, find
a. cosθ
b. sin2θ- cos2θ
c. Use tanθ to find the value of RQ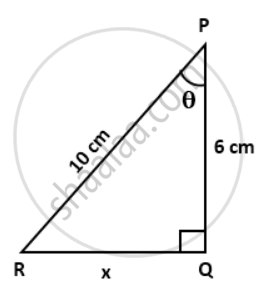
उत्तर
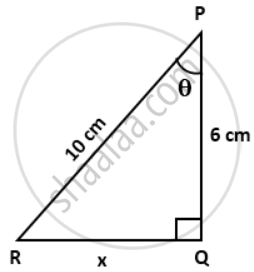
a cosθ = `"Base"/"Hypotenuse"`
⇒ cosθ
= `"PQ"/"PR"`
= `(6)/(10)`
= `(3)/(5)`
b. sin2θ + cos2θ = 1
⇒ `sin^2θ + (3/5)^2` = 1
⇒ `sin^2θ + (9)/(25)` = 1
⇒ sin2θ = `1 - (9)/(25) = (16)/(25)`
⇒ sinθ = `(4)/(5)`
∴ sin2θ - cos2θ
= `(6)/(25) - (9)/(5)`
= `(7)/(25)`
c. tanθ
= `(sinθ)/(cosθ)`
= `(4/5)/(3/5)`
= `(4)/(3)`
But,
tanθ = `"Perpendicular"/"Base" = "RQ"/"PQ"`
⇒ `"RQ"/"PQ" = (4)/(3)`
⇒ `"RQ"/(6) = (4)/(3)`
⇒ RQ
= `(4 xx 6)/(3)`
= 8cm.
APPEARS IN
संबंधित प्रश्न
Solve the following equation for A, if sin 3 A = `sqrt3 /2`
If 4 sin2 θ - 1= 0 and angle θ is less than 90°, find the value of θ and hence the value of cos2 θ + tan2θ.
Find the magnitude of angle A, if 2 sin A cos A - cos A - 2 sin A + 1 = 0
Solve for x : 2 cos 3x - 1 = 0
Solve the following equation for A, if 2cos2A = 1
Solve for x : 2 cos (3x - 15°) = 1
Find lengths of diagonals AC and BD. Given AB = 24 cm and ∠BAD = 60°.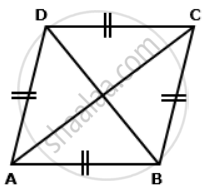
Evaluate the following: `(tan12°)/(cot78°)`
Evaluate the following: cos39° cos48° cos60° cosec42° cosec51°
Evaluate the following: `(5cot5° cot15° cot25° cot35° cot45°)/(7tan45° tan55° tan65° tan75° tan85°) + (2"cosec"12° "cosec"24° cos78° cos66°)/(7sin14° sin23° sec76° sec67°)`
