Advertisements
Advertisements
Question
Solve the following equation for A, if sec 2A = 2
Solution
According to the question,
We have,
sec 2A = 2
sec 2A = sec 60°
2A = 60°
A = 30°
APPEARS IN
RELATED QUESTIONS
State for any acute angle θ whether sin θ increases or decreases as θ increases
If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.
Find the value of 'A', if 2 cos A = 1
Find the value of 'A', if (1 - cosec A)(2 - sec A) = 0
If A = B = 60°, verify that: sin(A - B) = sinA cosB - cosA sinB
If θ < 90°, find the value of: sin2θ + cos2θ
Find the value of 'x' in each of the following: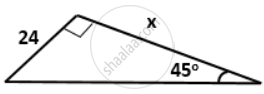
Find the length of EC.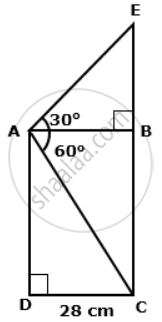
Evaluate the following: `(3sin37°)/(cos53°) - (5"cosec"39°)/(sec51°) + (4tan23° tan37° tan67° tan53°)/(cos17° cos67° "cosec"73° "cosec"23°)`
Evaluate the following: `(sin0° sin35° sin55° sin75°)/(cos22° cos64° cos58° cos90°)`
