Advertisements
Advertisements
Question
Find the value of 'x' in each of the following: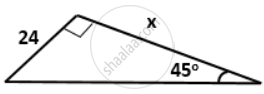
Solution
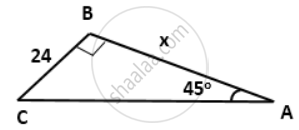
From the figure, we have
tan45° = `"BC"/"AB"`
⇒ 1 = `(24)/x`
⇒ x = 24.
APPEARS IN
RELATED QUESTIONS
Solve for x : cos `(x)/(3) –1` = 0
If `sqrt(2) = 1.414 and sqrt(3) = 1.732`, find the value of the following correct to two decimal places tan60°
Find the length of EC.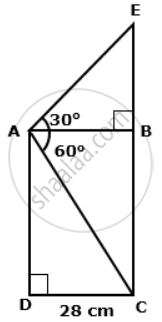
Evaluate the following: `(tan42°)/(cot48°) + (cos33°)/(sin57°)`
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: tan77° - cot63° + sin57°
Evaluate the following: `(3sin37°)/(cos53°) - (5"cosec"39°)/(sec51°) + (4tan23° tan37° tan67° tan53°)/(cos17° cos67° "cosec"73° "cosec"23°)`
If tan4θ = cot(θ + 20°), find the value of θ if 4θ is an acute angle.
If A, B and C are interior angles of ΔABC, prove that sin`(("A" + "B")/2) = cos "C"/(2)`
If P, Q and R are the interior angles of ΔPQR, prove that `cot(("Q" + "R")/2) = tan "P"/(2)`
Prove the following: `(tan(90° - θ)cotθ)/("cosec"^2 θ)` = cos2θ
