Advertisements
Advertisements
Question
Solve for x : 3 tan2 (2x - 20°) = 1
Solution
3 tan2 ( 2x – 20°) = 1
tan ( 2x – 20°) = `(1)/(sqrt3)`
tan ( 2x – 20°) = tan 30°
2x –20° = 30°
2x = 50°
x = 25°
APPEARS IN
RELATED QUESTIONS
From the given figure,
find:
(i) cos x°
(ii) x°
(iii) `(1)/(tan^2 xx°) – (1)/(sin^2xx°)`
(iv) Use tan xo, to find the value of y.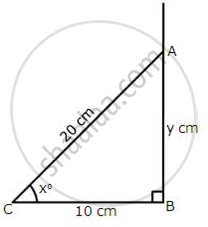
Solve for x : 2 cos 3x - 1 = 0
Find the magnitude of angle A, if tan A - 2 cos A tan A + 2 cos A - 1 = 0
Solve for x : sin2 60° + cos2 (3x- 9°) = 1
Evaluate the following: `((sin3θ - 2sin4θ))/((cos3θ - 2cos4θ))` when 2θ = 30°
If A = B = 60°, verify that: tan(A - B) = `(tan"A" - tan"B")/(1 + tan"A" tan"B"")`
Find the length of AD. Given: ∠ABC = 60°, ∠DBC = 45° and BC = 24 cm.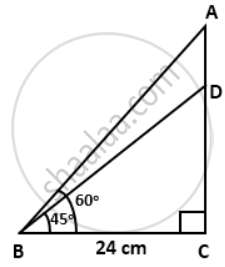
Find x and y, in each of the following figure: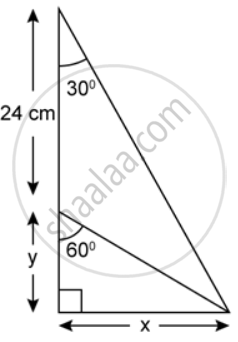
Evaluate the following: `(sin25° cos43°)/(sin47° cos 65°)`
Evaluate the following: cot27° - tan63°
