Advertisements
Advertisements
प्रश्न
Solve for x : 3 tan2 (2x - 20°) = 1
उत्तर
3 tan2 ( 2x – 20°) = 1
tan ( 2x – 20°) = `(1)/(sqrt3)`
tan ( 2x – 20°) = tan 30°
2x –20° = 30°
2x = 50°
x = 25°
APPEARS IN
संबंधित प्रश्न
Calculate the value of A, if cos 3A. (2 sin 2A - 1) = 0
Solve for x : sin2 60° + cos2 (3x- 9°) = 1
Evaluate the following: `((1 - cosθ)(1 + cosθ))/((1 - sinθ)(1 + sinθ)` if θ = 30°
If θ < 90°, find the value of: `tan^2θ - (1)/cos^2θ`
If `sqrt(3)`sec 2θ = 2 and θ< 90°, find the value of θ
Find x and y, in each of the following figure: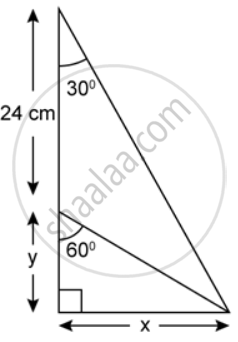
In right-angled triangle ABC; ∠B = 90°. Find the magnitude of angle A, if:
a. AB is `sqrt(3)` times of BC.
B. BC is `sqrt(3)` times of BC.
Evaluate the following: `(cos34° cos35°)/(sin57° sin56°)`
Evaluate the following: `(tan42°)/(cot48°) + (cos33°)/(sin57°)`
If A, B and C are interior angles of ΔABC, prove that sin`(("A" + "B")/2) = cos "C"/(2)`
