Question

समांतर चतुर्भुज के तीन शीर्ष बिंदुओं के निर्देशांक A(5, 6), B(1, -2) और C(3, -2) हों तो चौथे बिंदु के सभी निर्देशांकों की संभव जोड़ियाँ ज्ञात कीजिए। 

Answer 1

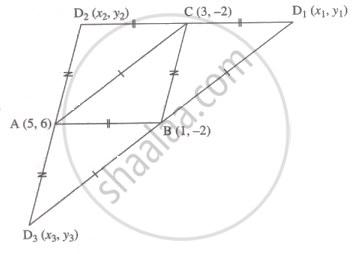
A(5, 6); B(1, -2) और C(3, -2).

दी गई आकृति के अनुसार बिंदु D के तीन संभव स्थान है | मानो कि वे तीन संभव बिंदु क्रमशः D₁(x₁, y₁); D₂(x₂, y₂) तथा D₃(x₃, y₃) हैं |

`square`ABD₁C एक समांतर चतुर्भुज है |

∴ AB = CD₁       ...(समांतर चतुर्भुज की सम्मुख भुजा)     ...(1)

`square`ABCD₂ भी एक समांतर चतुर्भुज है | 

∴ AB = CD₂        ...(समांतर चतुर्भुज की सम्मुख भुजा) ...(2)

∴ CD₁ = CD₂    ....[(1) और (2) से]

∴ बिंदु C रेख D₂D₁ का मध्यबिंदु है | 

इसी प्रकार बिंदु B रेख D₁D₃ का मध्यबिंदु है और बिंदु A रेख D₂D₃ का मध्यबिंदु है | 

अब, बिंदु C रेख D₂D₁ का मध्यबिंदु है |  

∴ मध्यबिंदु के सूत्र से, `3 = (x_2 + x_1)/2`

∴ `x_1 + x_2 = 6`     ...(3)

इसी प्रकार, `x_2 + x_3 = 10`    ...(4)

और `x_1 + x_3 = 2`      ...(5)

समीकरण (3), (4) और (5) को जोड़ने पर,

`x_1 + x_2 + x_2 + x_3 + x_1 + x_3 = 6 + 10 + 2`

∴ `2x_1 + 2x_2 + 2x_3 = 18`

∴ `2(x_1 + x_2 + x_3) = 18`

∴ `x_1 + x_2 + x_3 = 18/2`

∴ `x_1 + x_2 + x_3 = 9`       ...(6)

समीकरण (3) का मान समीकरण (6) में रखने पर,

`6 + x_3 = 9`

∴ `x_3 = 9 - 6`

∴ `x_3 = 3`

समीकरण (4) का मान समीकरण (6) में रखने पर,

`x_1 + 10 = 9`

∴ `x_1 = 9 - 10`

∴ `x_1 = -1`

समीकरण (5) का मान समीकरण (6) में रखने पर,

`x_2 + 2 = 9`

∴ `x_2 = 9 - 2`

∴ `x_2 = 7`

बिंदु C रेख D₂D₁ का मध्यबिंदु है | 

∴ मध्यबिंदु के सूत्र से,

`-2 = (y_1 + y_2)/2`

∴ `y_1 + y_2 = -4`       ...(7)

इसी प्रकार, `y_2 + y_3 = 12`      ....(8)

और `y_1 + y_3 = -4`       ...(9)

समीकरण (7), (8) और (9) को जोड़ने पर,

`y_1 + y_2 + y_2 + y_3 + y_1 + y_3 = -4 + 12 - 4`

∴ `2y_1 + 2y_2 + 2y_3 = 4`

∴ `2(y_1 + y_2 + y_3) = 4`

∴ `y_1 + y_2 + y_3 = 4/2`

∴ `y_1 + y_2 + y_3 = 2`          ...(10)

समीकरण (7) का मान समीकरण (10) में रखने पर,

`-4 + y_3 = 2`

∴ `y_3 = 2 + 4`

∴ `y_3 = 6`

समीकरण (8) का मान समीकरण (10) में रखने पर,

`y_1 + 12 = 2`

∴ `y_1 = 2 - 12`

∴ `y_1 = -10`

समीकरण (9) का मान समीकरण (10) में रखने पर,

`y_2 + (-4) = 2`

∴ `y_2 - 4 = 2`

∴ `y_2 = 2 + 4`

∴ `y_2 = 6`

बिंदु D₁ का निर्देशांक (-1, -10) है |

बिंदु D₂ का निर्देशांक (7, 6) है |

बिंदु D₃ का निर्देशांक (3, 6) है |

शीर्षबिंदु D के सभी निर्देशांकों की संभव जोड़ियाँ (-1, -10); (7, 6) और (3, 6) हैं |