Advertisements
Advertisements
प्रश्न
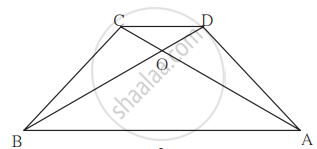
समलंब चौकोन ABCD मध्ये, बाजू AB || बाजू DC कर्ण AC व कर्ण BD हे परस्परांना O बिंदूत छेदतात. AB = 20, DC = 6, OB = 15 तर OD काढा.
उत्तर
बाजू AB || बाजू DC व रेख BD ही त्यांची छेदिका आहे. ......[पक्ष]
∴ ∠DBA ≅ ∠BDC .....[व्युत्क्रम कोन]
∴ ∠OBA ≅ ∠ODC ....(i) [D-O-B]
ΔOBA व ΔODC मध्ये,
∠OBA ≅ ∠ODC ......[(i) वरून]
∠BOA ≅ ∠DOC .......[विरुद्ध कोन]
∴ ΔOBA ∼ ΔODC .......[समरूपतेची कोको कसोटी]
∴ `"OB"/"OD" = "AB"/"DC"` .......[समरूप त्रिकोणांच्या संगत बाजू]
∴ `15/"OD" = 20/6`
∴ OD = `(15 xx 6)/20`
∴ OD = 4.5 एकक
APPEARS IN
संबंधित प्रश्न
आकृती मधील त्रिकोण समरूप आहेत का? असतील तर कोणत्या कसोटीनुसार?
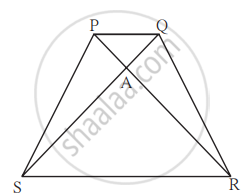
आकृतीत समलंब चौकोन PQRS मध्ये, बाजू PQ || बाजू SR, AR = 5AP, AS = 5AQ तर सिद्ध करा, SR = 5PQ.
आकृतीत रेख AC व रेख BD परस्परांना P बिंदूत छेदतात आणि `"AP"/"CP" = "BP"/"DP"` तर सिद्ध करा, ΔABP ∼ ΔCDP.
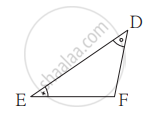
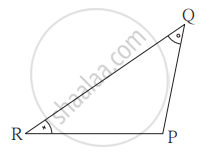
जर ΔDEF व ΔPQR मध्ये, ∠D ≅ ∠Q, ∠R ≅ ∠E, तर खालीलपैकी असत्य विधान कोणते?
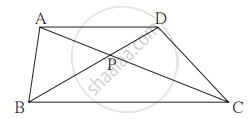
`square`ABCD मध्ये रेख AD || रेख BC. कर्ण AC आणि कर्ण BD परस्परांना बिंदू P मध्ये छेदतात. तर दाखवा की `"AP"/"PD" = "PC"/"BP"`
आकृती मध्ये XY || बाजू AC. जर 2AX = 3BX आणि XY = 9 तर AC ची किंमत काढण्यासाठी खालील कृती पूर्ण करा.

कृती : 2AX = 3BX
∴ `"AX"/"BX" = square/square`
`("AX" + "BX")/"BX" = (square + square)/square` ......(योग क्रिया करून)
`"AB"/"BX" = square/square` ......(I)
ΔBCA ~ ΔBYX .......(समरूपतेची `square` कसोटी)
∴ `"BA"/"BX" = "AC"/"XY"` ..........(समरूप त्रिकोणाच्या संगत बाजू)
∴ `square/square = "AC"/9`
∴ AC = `square` ..........(I) वरून
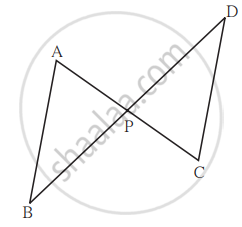
आकृतीमध्ये रेख AC व रेख BD परस्परांना P बिंदूत छेदतात आणि `"AP"/"PC" = "BP"/"PD"`, तर सिद्ध करा ∆ABP ~ ∆CDP.
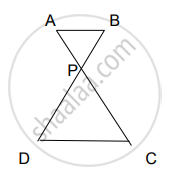
आकृतीमध्ये समलंब चौकोन PQRS मध्ये बाजू PQ || बाजू SR, AR = 5 AP, तर सिद्ध करा, SR = 5 PQ.
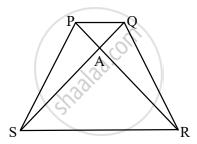

वरील आकृतीत रेख AC आणि रेख BD परस्परांना P बिंदूत छेदतात. जर `"AP"/"CP" = "BP"/"DP"` तर ΔABP ∼ ΔCDP दाखवण्यासाठी खालील कृती पूर्ण करा.
कृती: ΔABP व ΔCDP मध्ये
`"AP"/"CP" = "BP"/"DP" ....square`
∠APB ≅ `square` ...... विरुद्ध कोन
∴ `square` ∼ ΔCDP ....... समरूपतेची `square` कसोटी.

वरील आकृतीत, ΔABC मध्ये रेख XY || बाजू AC, जर 2AX = 3BX आणि XY = 9, तर AC ची किंमत काढा.
