Advertisements
Advertisements
प्रश्न
Solve the following systems of equations:
`x/3 + y/4 =11`
`(5x)/6 - y/3 = -7`
उत्तर
The given equations are:
`x/3 + y/4 =11`...(i)
`(5x)/6 - y/3 = -7` .....(ii)
From (i) we get
`(4x + 3y)/12 = 11`
=> 4x + 3y = 132 ....(iii)
From (ii), we get
`(5x + 2y)/6 = -7`
=> 5x - 2y = -42 ....(iv)
Let us eliminate y from the given equations. The coefficients of y in the equations(iii) and (iv) are 3 and 2 respectively. The L.C.M of 3 and 2 is 6. So, we make the coefficient of y equal to 6 in the two equations.
Multiplying (iii) by 2 and (iv) by 3, we get
8x + 6y = 264 ...(v)
15x - 6x = -126 ...(vi)
Adding (v) and (vi), we get
8x + 15x = 264 - 126
=> 23x = 138
`=> x = 138/23 = 6`
Substituting x = 6 in (iii), we get
4 x 6 + 3y = 132
=> 3y = 132 - 24
3y = 108
`=> y = 108/3 = 36`
Hence, the solution of the given system of equations is x = 6, y = 36.
APPEARS IN
संबंधित प्रश्न
A thief, after committing a theft, runs at a uniform speed of 50 m/minute. After 2 minutes, a policeman runs to catch him. He goes 60 m in first minute and increases his speed by 5 m/minute every succeeding minute. After how many minutes, the policeman will catch the thief?
Solve the following system of equations by cross-multiplication method ax + by = 1; `bx + ay = \frac{(a+b)^{2}}{a^{2}+b^{2}-1`
Solve the following systems of equations:
4u + 3y = 8
`6u - 4y = -5`
Solve each of the following systems of equations by the method of cross-multiplication
3x + 2y + 25 = 0
2x + y + 10 = 0
Solve each of the following systems of equations by the method of cross-multiplication
`x/a + y/b = a + b`
Solve each of the following systems of equations by the method of cross-multiplication :
mx – my = m2 + n2
x + y = 2m
Find the values of x and y in the following rectangle [see figure].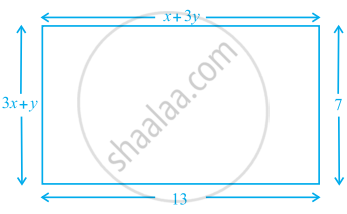
Solve the following pair of equations:
`x/a + y/b = a + b, x/a^2 + y/b^2 = 2, a, b ≠ 0`
Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively. She received Rs 1860 as annual interest. However, had she interchanged the amount of investments in the two schemes, she would have received Rs 20 more as annual interest. How much money did she invest in each scheme?
Anuj had some chocolates, and he divided them into two lots A and B. He sold the first lot at the rate of ₹ 2 for 3 chocolates and the second lot at the rate of ₹ 1 per chocolate, and got a total of ₹ 400. If he had sold the first lot at the rate of ₹ 1 per chocolate, and the second lot at the rate of ₹4 for 5 chocolates, his total collection would have been ₹460. Find the total number of chocolates he had.
