Advertisements
Advertisements
प्रश्न
Solve the following problem :
Minimize Z = 2x + 3y Subject to x – y ≤ 1, x + y ≥ 3, x ≥ 0, y ≥ 0
उत्तर
To find the graphical solution, construct the table as follows:
| Inequation | Equation | Double intercept form | Points (x1, x2) | Region |
| x – y ≤ 1 | x – y = 1 | `x/(1) + y/(-1)` = 1 | A (1, 0) B (0, –1) |
0 – 0 ≤ 1 |
| x + y ≥ 1 | x + y = 3 | `x/(3) + y/(3)` = 1 | C (3, 0) D (0, 3) |
0 + 0 ≥ 3 ∴ 0 ≥ 3 ∴ non-origin side |
| x ≥ 0 | x = 0 | – | R.H.S. of Y- axis | |
| y ≥ | y = 0 | above X-axis |
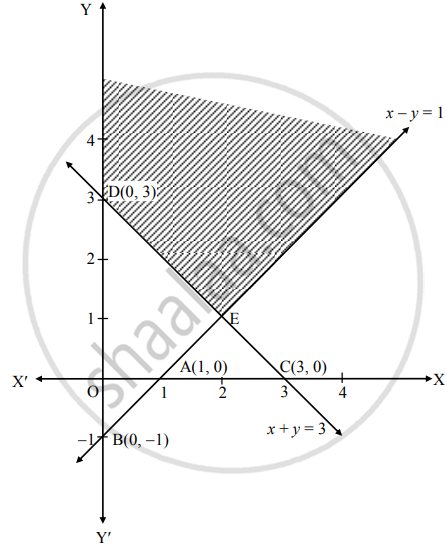
The shaded portion Y' DE is the feasible region.
Whose vertices are D(0, 3) and E
E is the point of intersection of lines
x – y = 1 …(i)
x + y = 3 …(ii)
∴ By (i) + (ii), we get
x – y = 1
x + y = 3
2x = 4
∴ x = `(4)/(2)` = 2
Substituting x = 2 in (i), we get
2 – y = 1
∴ y = 1
∴ E(2, 1)
Here, the objective function is Z = 2x + 3y
Now, we will find minimum value of Z as follows:
| Feasible points | The value of Z = 2x + 3y |
| D(0, 3) | Z = 2(0) + 3(3) = 9 |
| E(2, 1) | Z = 2(2) + 3(1) = 4 + 3 = 7 |
∴ Z has minimum value 7 at E(2, 1)
∴ Z is minimum, when x = 2, y = 1.
APPEARS IN
संबंधित प्रश्न
A firm manufactures 3 products A, B and C. The profits are Rs 3, Rs 2 and Rs 4 respectively. The firm has 2 machines and below is the required processing time in minutes for each machine on each product :
| Machine | Products | ||
| A | B | C | |
| M1 M2 |
4 | 3 | 5 |
| 2 | 2 | 4 | |
Machines M1 and M2 have 2000 and 2500 machine minutes respectively. The firm must manufacture 100 A's, 200 B's and 50 C's but not more than 150 A's. Set up a LPP to maximize the profit.
Amit's mathematics teacher has given him three very long lists of problems with the instruction to submit not more than 100 of them (correctly solved) for credit. The problem in the first set are worth 5 points each, those in the second set are worth 4 points each, and those in the third set are worth 6 points each. Amit knows from experience that he requires on the average 3 minutes to solve a 5 point problem, 2 minutes to solve a 4 point problem, and 4 minutes to solve a 6 point problem. Because he has other subjects to worry about, he can not afford to devote more than
Choose the correct alternative:
The value of objective function is maximize under linear constraints.
Choose the correct alternative :
The maximum value of z = 5x + 3y. subject to the constraints
Fill in the blank :
Graphical solution set of the in equations x ≥ 0, y ≥ 0 is in _______ quadrant
State whether the following is True or False :
The region represented by the inqualities x ≤ 0, y ≤ 0 lies in first quadrant.
Solve the following problem :
Minimize Z = 4x + 2y Subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0, y ≥ 0
Choose the correct alternative:
If LPP has optimal solution at two point, then
Choose the correct alternative:
The minimum value of Z = 4x + 5y subjected to the constraints x + y ≥ 6, 5x + y ≥ 10, x, y ≥ 0 is
Choose the correct alternative:
The point at which the minimum value of Z = 8x + 12y subject to the constraints 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0 is obtained at the point
Choose the correct alternative:
The corner points of the feasible region are (0, 3), (3, 0), (8, 0), `(12/5, 38/5)` and (0, 10), then the point of maximum Z = 6x + 4y = 48 is at
State whether the following statement is True or False:
The maximum value of Z = 5x + 3y subjected to constraints 3x + y ≤ 12, 2x + 3y ≤ 18, 0 ≤ x, y is 20
A set of values of variables satisfying all the constraints of LPP is known as ______
The feasible region represented by the inequations x ≥ 0, y ≤ 0 lies in ______ quadrant.
A chemist has a compound to be made using 3 basic elements X, Y, Z so that it has at least 10 litres of X, 12 litres of Y and 20 litres of Z. He makes this compound by mixing two compounds (I) and (II). Each unit compound (I) had 4 litres of X, 3 litres of Y. Each unit compound (II) had 1 litre of X, 2 litres of Y and 4 litres of Z. The unit costs of compounds (I) and (II) are ₹ 400 and ₹ 600 respectively. Find the number of units of each compound to be produced so as to minimize the cost
Maximize Z = 400x + 500y subject to constraints
x + 2y ≤ 80, 2x + y ≤ 90, x ≥ 0, y ≥ 0
Minimize Z = 2x + 3y subject to constraints
x + y ≥ 6, 2x + y ≥ 7, x + 4y ≥ 8, x ≥ 0, y ≥ 0
Solve the following LPP graphically:
Maximize Z = 9x + 13y subject to constraints
2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequation | Equation | X intercept | Y intercept | Region |
| 2x + 3y ≤ 18 | 2x + 3y = 18 | (9, 0) | (0, ___) | Towards origin |
| 2x + y ≤ 10 | 2x + y = 10 | ( ___, 0) | (0, 10) | Towards origin |
| x ≥ 0, y ≥ 0 | x = 0, y = 0 | X axis | Y axis | ______ |
The feasible region is OAPC, where O(0, 0), A(0, 6),
P( ___, ___ ), C(5, 0)
The optimal solution is in the following table:
| Point | Coordinates | Z = 9x + 13y | Values | Remark |
| O | (0, 0) | 9(0) + 13(0) | 0 | |
| A | (0, 6) | 9(0) + 13(6) | ______ | |
| P | ( ___,___ ) | 9( ___ ) + 13( ___ ) | ______ | ______ |
| C | (5, 0) | 9(5) + 13(0) | ______ |
∴ Z is maximum at __( ___, ___ ) with the value ___.
If z = 200x + 500y .....(i)
Subject to the constraints:
x + 2y ≥ 10 .......(ii)
3x + 4y ≤ 24 ......(iii)
x, 0, y ≥ 0 ......(iv)
At which point minimum value of Z is attained.
