Advertisements
Advertisements
प्रश्न
Solve the following question using appropriate Euclid’s axiom:
Look at the figure. Show that length AH > sum of lengths of AB + BC + CD.

उत्तर
Given in the question, AB, BC and CD are parts of line.
Then, AB + BC + CD = AD ...(i)
And AD is the part of line AH.
Now, By Euclid’s axiom 5, the whole is greater than the part.
So, AH > AD
That is length AH > sum of length of AB + BC + CD ...[By using (i)]
APPEARS IN
संबंधित प्रश्न
If a point C lies between two points A and B such that AC = BC, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Greek’s emphasised on ______.
The things which are double of the same thing are equal to one another.
If a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AB = BC, BX = BY. Show that AX = CY.
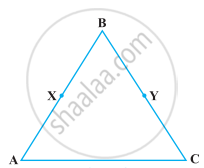
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC.
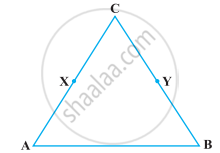
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have ∠1 = ∠3 and ∠2 = ∠4. Show that ∠A = ∠C.
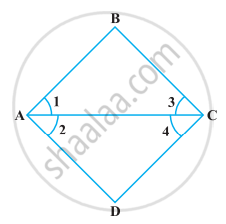
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have ∠ABC = ∠ACB, ∠3 = ∠4. Show that ∠1 = ∠2.

The following statement is true or false? Give reason for your answer.
There are an infinite number of lines which pass through two distinct points.
The following statement is true or false? Give reason for your answer.
If two circles are equal, then their radii are equal.
