Advertisements
Advertisements
प्रश्न
Subtract:
\[\frac{ab}{7} - \frac{35}{3}bc + \frac{6}{5}ac \text { from } \frac{3}{5}bc - \frac{4}{5}ac\]
उत्तर
\[ \left( \frac{3}{5}bc - \frac{4}{5}ac \right) - \left( \frac{ab}{7} - \frac{35}{3}bc + \frac{6}{5}ac \right)\]
\[ = \frac{3}{5}bc - \frac{4}{5}ac - \frac{ab}{7} + \frac{35}{3}bc - \frac{6}{5}ac\]
\[ = \frac{3}{5}bc + \frac{35}{3}bc - \frac{4}{5}ac - \frac{6}{5}ac - \frac{ab}{7} (\text { Collecting like terms })\]
\[ = \frac{184}{15}bc - 2ac - \frac{ab}{7} (\text { Combining like terms })\]
APPEARS IN
संबंधित प्रश्न
Subtract: 4a − 7ab + 3b + 12 from 12a − 9ab + 5b − 3
Subtract 4p2q − 3pq + 5pq2 − 8p + 7q − 10 from 18 − 3p − 11q + 5pq − 2pq2 + 5p2q
Simplify combining like terms: 3a - 2b - ab - (a - b + ab) + 3ab + b - a
Add: 3p2q2 - 4pq + 5, - 10p2q2, 15 + 9pq + 7p2q2
Add: x2 - y2 - 1 , y2 - 1 - x2, 1- x2 - y2
Subtract: -m2 + 5mn from 4m2 - 3mn + 8
What should be added to x2 + xy + y2 to obtain 2x2 + 3xy?
Add: −9y, 11y, 2y
Find the sum of the following expressions
u + v, u – v, 2u + 5v, 2u – 5v
Each symbol given below represents an algebraic expression:
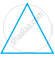= 2x2 + 3y, 
= 5x2 + 3x, 
= 8y2 – 3x2 + 2x + 3y
The symbols are then represented in the expression:
Find the expression which is represented by the above symbols.
