Advertisements
Advertisements
प्रश्न
Two adjacent angles of a parallelogram are (3x − 4)° and (3x + 10)°. Find the angles of the parallelogram.
उत्तर
\[\text{ We know that the adjacent angles of a parallelogram are supplementry } . \]
\[\text{ Hence }, \left( 3x + 10 \right)° \text{ and } \left( 3x - 4 \right)° \text{ are supplementry } . \]
\[\left( 3x + 10 \right)°+ \left( 3x - 4 \right)° = 180°\]
\[6x° + 6°= 180°\]
\[6x° = 174°\]
\[x = 29°\]
\[\text{ First angle } = \left( 3x + 10 \right)°= \left( 3 \times 29° + 10° \right) = 97°\]
\[\text{ Second angle }= \left( 3x - 4 \right)° = 83°\]
\[\text{ Thus, the angles of the parallelogram are } 97°, 83°, 97° \text{ and } 83°.\]
APPEARS IN
संबंधित प्रश्न
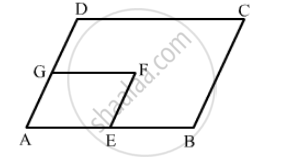
In the following figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
Which of the following statement is true for a rectangle?
Its diagonals are equal and perpendicular, and bisect each other.
Which of the following statement true for a square?
Its diagonals are equal to its sides.
Fill in the blank of the following, so as to make the statement true:
A square is a rectangle in which .....
Draw a square whose each side measures 4.8 cm.
State with Reason Whether the Following Statement is ‘True’ Or ‘False’.
Every rectangle is a parallelogram.
If diagonal of a rectangle is 26 cm and one side is 24 cm, find the other side.
Show that the bisectors of angles of a parallelogram form a rectangle
In a rectangle ABCD, AB = 25 cm and BC = 15. In what ratio does the bisector of ∠C divide AB?
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
