Advertisements
Advertisements
प्रश्न
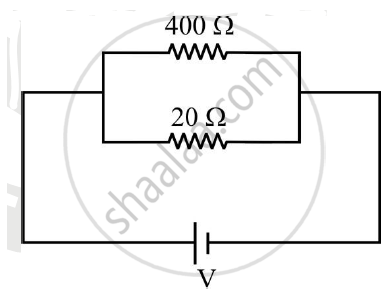
Two resistors R1 = 400Ω and R2 = 20 n are connected in parallel to a battery. If heating the power developed in R1 is 25 W. find the heating power developed in R2
उत्तर
`Power across `R_1` = 25 W
`P = V^2/R`
`25 xx 20 = V^2`
`V^2 = 500`
`V = sqrt500 V`
Power across `R_2` `P = V^2/R` = `500/400 = 1.2 W`
`V = sqrt500` as potential in parallel remain constant.
APPEARS IN
संबंधित प्रश्न
Two resistances R and 2R are connected in parallel in an electric circuit. The thermal energy developed in R and 2R are in the ratio _______________ .
Which of the following quantities does not change when a resistor connected to a battery is heated due to the current?
The emf ε and the internal resistance r of the battery, shown in the figure, are 4.3 V and 1.0 Ω respectively. The external resistance R is 50 Ω. The resistances of the ammeter and voltmeter are 2.0 Ω and 200 Ω respectively. (a) Find the readings of the two meters. (b) The switch is thrown to the other side. What will be the readings of the two meters now?

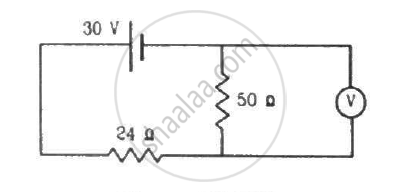
The voltmeter shown in the figure reads 18 V across the 50 Ω resistor. Find the resistance of the voltmeter.
Two resistors R1= 60 Ω and R2 = 90Ω are connected in parallel. If electric power consumed by the resistor R1 is15 W, calculate the power consumed by the resistor R2.
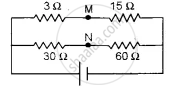
How much resistance should be connected to 15 Ω resistor shown in the circuit in figure below so that the points M and N are at the same potential:
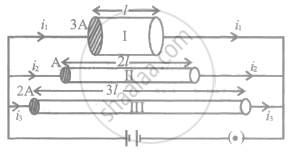
The figure shows three conductors I, II and III of same material, different lengths l, 2l and 3l and of different areas of cross-sections 3A, A and 2A respectively. Arrange them in the increasing order of current drawn from the battery.
The equivalent resistance of resistors connected in series is always ______
Let there be n resistors R1............Rn with Rmax = max (R1......... Rn) and Rmin = min {R1..... Rn}. Show that when they are connected in parallel, the resultant resistance RP < R min and when they are connected in series, the resultant resistance RS > Rmax. Interpret the result physically.
Eight identical cells, each of emf 2V and internal resistance 3 Ω, are connected in series to form a row. Six such rows are connected in parallel to form a battery. This battery is now connected to an external resistor R of resistance 6 Ω. Calculate:
- emf of the battery.
- internal resistance of the battery.
- current flowing through R.
