Question

Using this principle draw a diagram to show how a plane wave front incident at the interface of the two media gets refracted when it propagates from a rarer to a denser medium. Hence verify Snell's law of refraction.

Answer 1

Huygens’ Principle:

• Each point on the primary wave front acts as a source of secondary wavelets, sending out disturbance in all directions in a similar manner as the original source of light does.

• The new position of the wave front at any instant (called secondary wave front) is the envelope of the secondary wavelets at that instant.

Refraction On The Basis Of Wave Theory

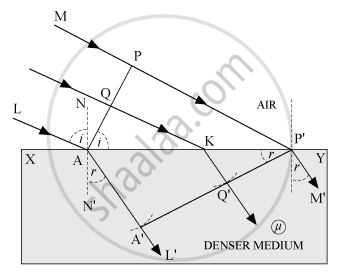
• Consider any point Q on the incident wave front.

• Suppose when disturbance from point P on incident wave front reaches point P'on the refracted wave front, the disturbance from point Q reaches Q' on the refracting surface XY.

• Since P'A'epresents the refracted wave front, the time taken by light to travel from a point on incident wave front to the corresponding point on refracted wave front should always be the same. Now, time taken by light to go from Q to Q' will be `t = (QK)/c + (KQ)/v  ...(1)`

In right-angled ΔAQK, ∠QAK = i

∴ QK = AK sin i … (2)

In right-angled ΔP'Q'K, ∠Q'P'K, = r and KQ = KP sin r…. (3)

Substituting (2) and (3) in equation (1),

`t = (AK sin i)/c + (KP'sin r)/v`

or, `(AK sin i)/c + ((AP' - AK)sin r)/v` (∵ KP' = AP' -AK)

or,`t = (AP')/c  sinr + AK ((sin i )/c - (sin r)/v)    ...... (4)`

The rays from different points on the incident wave front will take the same time to reach the corresponding points on the refracted wave front i.e., t given by equation (iv) is independent of AK. It will happen so, if`(sin i)/c -(sin r)/v =0 ⇒ (sini)/(sinr) =c/v ⇒μ = (sini)/(sinr) `

This is the Snell’s law for refraction of light.