Advertisements
Advertisements
प्रश्न
वक्र y2 = 4x और x2 = 4y से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
उत्तर
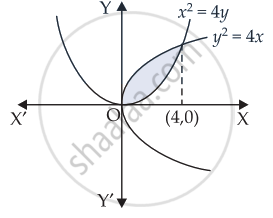
हमें प्राप्त है: y2 = 4x और x2 = 4y.
y = `x^2/4`
⇒ `(x^2/4)^2` = 4x
⇒ `x^4/16` = 4x
⇒ x4 = 64x
⇒ x4 – 64x = 0
⇒ x(x3 – 64) = 0
∴ x = 0, x = 4
वाँछित क्षेत्रफल = `int_0^4 sqrt(4x) "d"x - int_0^4 x^2/4 "d"x`
= `2 int_0^4 sqrt(x) "d"x - 1/4 int_0^4 x^2 "d"x`
= `2 * 2/3 [x^(3/2)]_0^4 - 1/4 * 1/3 [x^3]_0^4`
= `4/3 [(4)^(3/2) - 0] - 1/12 [(4)^3 - 0]`
= `4/3 [8] - 1/12[64]`
= `32/2 - 16/3`
= `16/3` वर्ग इकाई
इस प्रकार, वाँछित क्षेत्रफल = `16/3` वर्ग इकाई
APPEARS IN
संबंधित प्रश्न
समाकलन विधि का उपयोग करते हुए वक्र |x| + |y| = 1से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
समाकलन विधि का उपयोग करते हुए एक ऐसे त्रिभुज ABC का क्षेत्रफल ज्ञात कीजिए जिसके शीर्षों के निर्देशांक A(2, 0), B (4, 5) एवं C (6, 3) हैं।
समाकलन विधि का उपयोग करते हुए, रेखाओं 2x + y = 4, 3x – 2y = 6 एवं x – 3y + 5 = 0 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
0 और π के बीच, वक्र y = sin x का क्षेत्रफल ज्ञात कीजिए।

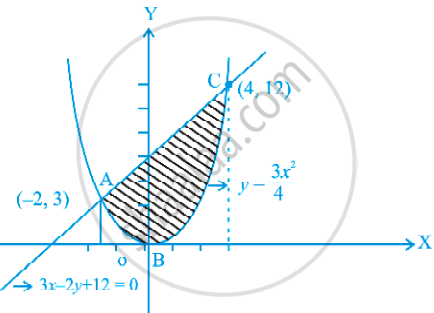
उस क्षेत्र का क्षेत्रफल ज्ञात कीजिए, जो परवलय y = `(3x^2)/4` और रेखा 3x - 2y + 12 = 0 के बीच में परिबद्ध है।
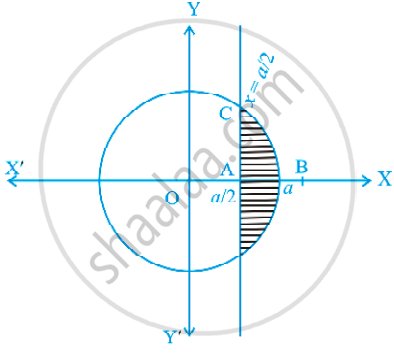
रेखा x = `"a"/2` द्वारा वृत्त x2 + y2 = a2 के काटे गए एक लघु वृत्तखंड का क्षेत्रफल ज्ञात कीजिए।
वृत्त x2 + y2 = 2 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल बराबर है
दीर्घवृत्त `x^2/"a"^2 + y^2/"b"^2` = 1 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल बराबर है
वक्र x = y2 , y-अक्ष तथा रेखा y = 3 और y = 4 से परिबद्ध क्षेत्र का क्षेत्रफल ______ है।
वक्र y2 = 9x, और y = 3x से परिबद्ध क्षेत्रफल का क्षेत्रफल ज्ञात कीजिए।
परवलय y2 = 2px, और x2 = 2py से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
y2 = 9x और y = x बीच में पड़ने वाले क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
परवलय x2 = y और रेखा y = x + 2 से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
क्षेत्र `{(x, 0) : y = sqrt(4 - x^2)}` और x-अक्ष का चित्रण कीजिए। समाकलन का उपयोग करते हुए इस क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = `sqrt(x - 1)` का अंतराल [1, 5] में एक संभावित आकृति खींचिए। इस वक्र के अंतर्गत तथा x = 1 और x = 5 रेखाओं के बीच के क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = `sqrt("a"^2 - x^2)` के अंतर्गत तथा x = 0 और x = a रेखाओं के बीच के क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
x = 0 और x = 2π के बीच वक्र y = sinx द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
समाकलन का प्रयोग करते हुए, उस त्रिभुज द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए, जिसके शीर्ष (-1, 1), (0, 5) और (3, 2) हैं।
क्षेत्र `{(x, "y") : "y"^2 ≤ 6"a"x "और" x^2 + "y"^2≤ 16"a"^2}` का एक संभावित आकृति खींचिए। साथ ही,समाकलन की विधि द्वारा इस क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
रेखाओं y = 4x + 5, y = 5 – x और 4y = x + 5 से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = 2cosx तथा x-अक्ष द्वारा x = 0 से x = 2π तक परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = 1 + |x +1|, x = –3, x = 3 तथा y = 0 का एक संभावित आकृति खींचिए। समाकलन का प्रयोग करते हुए, इन से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
प्रथम चतुर्थाश में, x-अक्ष, रेखा y = x और वृत्त x2 + y2 = 32 द्वारा घिरे क्षेत्र का क्षेत्रफल है-
परवलय y2 = x और सरल रेखा 2y = x से परिबद्ध क्षेत्र का क्षेत्रफल है
दीर्घवृत्त `x^2/25 + "y"^2/16` = 1 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र y = x + 1 तथा x = 2 और x = 3 रेखाओं द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र x = 2y + 3 तथा y = 1 और y = –1 रेखाओं द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
