Advertisements
Advertisements
प्रश्न
What is the net flux of the uniform electric field of previous question through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
उत्तर
All the faces of a cube are parallel to the coordinate axes. Therefore, the number of field lines entering the cube is equal to the number of field lines piercing out of the cube. As a result, net flux through the cube is zero.
APPEARS IN
संबंधित प्रश्न
Define electric flux.
Given the electric field in the region `vecE=2xhati`, find the net electric flux through the cube and the charge enclosed by it.
Consider a uniform electric field E = 3 × 103 `bbhat i` N/C.
- What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane?
- What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
Define Electric Flux. Write its SI unit.
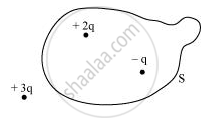
Figure shows three point charges +2q, −q and + 3q. Two charges + 2q and −q are enclosed within a surface ‘S’. What is the electric flux due to this configuration through the surface ‘S’?
A circular ring of radius r made of a non-conducting material is placed with its axis parallel to a uniform electric field. The ring is rotated about a diameter through 180°. Does the flux of the electric field change? If yes, does it decrease or increase?
It is said that any charge given to a conductor comes to its surface. Should all the protons come to the surface? Should all the electrons come to the surface? Should all the free electrons come to the surface?
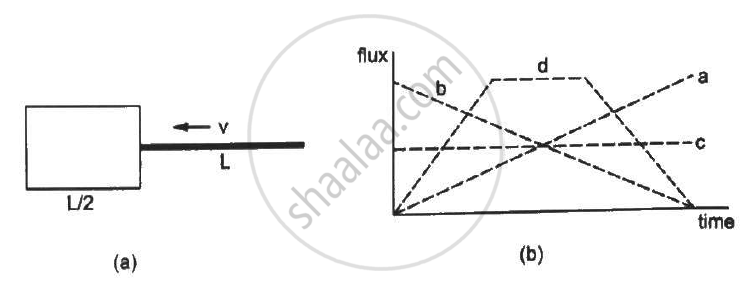
Following Figure (a) shows an imaginary cube of edge L/2. A uniformly charged rod of length (L) moves towards the left at a small but constant speed `nu.` At t = 0, the left end just touches the centre of the face of the cube opposite it. Which of the graphs shown in the figure (b) represents the flux of the electric field through the cube as the rod goes through it?
If the flux of the electric field through a closed surface is zero,
(a) the electric field must be zero everywhere on the surface
(b) the electric field may be zero everywhere on the surface
(c) the charge inside the surface must be zero
(d) the charge in the vicinity of the surface must be zero
A uniform electric field of intensity 400 N/C, exists in a certain region. How much flux will cross a given area of 10 cm2 in this region, if the area vector is inclined at 60° to the direction of the field?
A charge 'Q' µC is placed at the centre of a cube. The flux through one face and two opposite faces of the cube is respectively ______.
The electric flux through the surface ______.
 |
 |
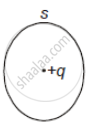 |
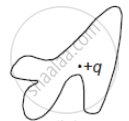 |
| (i) | (ii) | (iii) | (iv) |
A point charge q is placed at a distance a/2 directly above the centre of a square of side a. The electric flux through the square is ______.
In a region of space having a uniform electric field E, a hemispherical bowl of radius r is placed. The electric flux Φ through the bowl is:
An electric charge q is placed at the center of a cube of side ℓ. The electric flux on one of its faces will be ______.
The S.I. unit of electric flux is ______
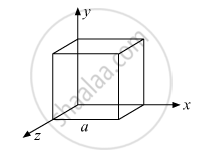
What will be the total flux through the faces of the cube (figure) with side of length a if a charge q is placed at

- A: a corner of the cube.
- B: mid-point of an edge of the cube.
- C: centre of a face of the cube.
- D: mid-point of B and C.
