Advertisements
Advertisements
प्रश्न
When a block a mass M is suspended by a long wire of length L, the elastic potential potential energy stored in the wire is `1/2` × stress × strain × volume. Show that it is equal to `1/2` Mgl, where l is the extension. The loss in gravitational potential energy of the mass earth system is Mgl. Where does the remaining `1/2` Mgl energy go ?
उत्तर
Let the CSA of the wire be A.
\[\text{ Stress }= \frac{\text{ Force }}{\text{ Area }} = \frac{\text{ Mg }}{\text{ A }}\]
\[\text{ Strain }= \frac{\text{l}}{\text{L}}\]
\[\text{ Volume = AL} \]
\[ \text{ We need to calculate the elastic potential energy stored in the wire which is given to be equal to }\frac{1}{2} \times \text{ Stress } \times \text{ Strain } \times \text{ Volume } . \]
\[\text{ Elastic potential energy }= \frac{1}{2} \times \text{ Stress }\times \text{ Strain } \times \text{ Volume }\]
\[ = \frac{1}{2} \times \frac{Mg}{A} \times \frac{l}{L} \times AL\]
\[ = \frac{1}{2}Mgl\]
The other \[\frac{1}{2}Mgl\] is converted into kinetic energy of the mass.
When the mass leaves its initial point on the spring, it acquires a velocity as it moves down. The velocity reaches its maximum at the end point. The spring oscillates. Finally, when the kinetic energy is dissipated into heat, the spring comes to rest.
APPEARS IN
संबंधित प्रश्न
A steel cable with a radius of 1.5 cm supports a chairlift at a ski area. If the maximum stress is not to exceed 108 N m–2, what is the maximum load the cable can support?
A rigid bar of mass 15 kg is supported symmetrically by three wires each 2.0 m long. Those at each end are of copper and the middle one is of iron. Determine the ratio of their diameters if each is to have the same tension.
A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10–2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6.0 mm. What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9 × 107 Pa? Assume that each rivet is to carry one-quarter of the load.
The ratio stress/strain remain constant for small deformation of a metal wire. When the deformation is made larger, will this ratio increase or decrease?
The yield point of a typical solid is about 1%. Suppose you are lying horizontally and two persons are pulling your hands and two persons are pulling your legs along your own length. How much will be the increase in your length if the strain is 1% ? Do you think your yield point is 1% or much less than that?
The breaking stress of a wire depends on
When a metal wire is stretched by a load, the fractional change in its volume ∆V/V is proportional to
Answer in one sentence.
Define strain.
A charged particle is moving in a uniform magnetic field in a circular path of radius R. When the energy of the particle becomes three times the original, the new radius will be ______.
A spiral spring is stretched by a weight. The strain will be:
A rod has a radius of 100 mm and a length of 10 cm. A 100 N force compress along its length. Calculate the longitudinal stress developed in the rod.
A rectangular frame is to be suspended symmetrically by two strings of equal length on two supports (Figure). It can be done in one of the following three ways;
| (a) |  |
| (b) |  |
| (c) |  |
The tension in the strings will be ______.
Is stress a vector quantity?
Consider a long steel bar under a tensile stress due to forces F acting at the edges along the length of the bar (Figure). Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane
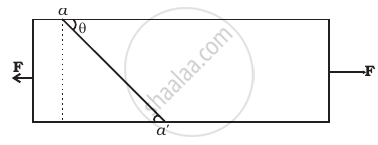
- For what angle is the tensile stress a maximum?
- For what angle is the shearing stress a maximum?
If 'S' is stress and 'Y' is young's modulus of the material of a wire, the energy stored in the wire per unit volume is ______.
The area of the cross-section of the rope used to lift a load by a crane is 2.5 × 10-4m2. The maximum lifting capacity of the crane is 10 metric tons. To increase the lifting capacity of the crane to 25 metric tons, the required area of cross-section of the rope should be ______.
(take g = 10 ms-2)
What is an elastomer?
Answer in one sentence:
What is an elastomer?
