Advertisements
Advertisements
प्रश्न
Write the truth value of the following statement.
A quadratic equation has two distinct roots or 6 has three prime factors.
उत्तर
Let p : A quadratic equation has two distinct roots.
q : 6 has three prime factors.
The truth values of p and q are F and F respectively.
The given statement in symbolic form is p ∨ q.
∴ p ∨ q ≡ F ∨ F ≡ F
∴ Truth value of the given statement is F.
APPEARS IN
संबंधित प्रश्न
Using truth table prove that ∼p ˄ q ≡ (p ˅ q) ˄ ∼p
Evaluate: ∫ x . log x dx
Write the following compound statement symbolically.
If Δ ABC is right-angled at B, then m∠A + m∠C = 90°
Construct the truth table of the following statement pattern.
(p ∧ q) ↔ (q ∨ r)
Construct the truth table of the following statement pattern.
(q → p) ∨ (∼ p ↔ q)
Construct the truth table of the following statement pattern.
[p → (q → r)] ↔ [(p ∧ q) → r]
Determine the truth values of p and q in the following case:
(p ∨ q) is T and (p ∧ q) is T
Express the following statement in symbolic form.
Even though it is cloudy, it is still raining.
Write the truth value of the following statement.
Earth is a planet and Moon is a star.
Write the negation of the following statement.
All men are animals.
Write the truth value of the negation of the following statement.
For every x ∈ N, x + 3 < 8.
Write the following statement in symbolic form.
Even though it is not cloudy, it is still raining.
Find the truth value of the following statement.
3 is a prime number and an odd number.
If p and q are true and r and s are false, find the truth value of the following compound statement.
p ∧ (q ∧ r)
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If a real number is not rational, then it must be irrational.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
Proof is lengthy and it is not interesting.
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If price increases, then demand falls.
Consider the following statements.
- If D is dog, then D is very good.
- If D is very good, then D is dog.
- If D is not very good, then D is not a dog.
- If D is not a dog, then D is not very good.
Identify the pairs of statements having the same meaning. Justify.
Write the negation of the following statement.
∀ n ∈ N, n + 3 > 9.
The negation of the statement (p ˄ q) `→` (r ˅ ∼ p) is ______.
Write the negation of the statement “An angle is a right angle if and only if it is of measure 90°”
Write the following statements in symbolic form
Milk is white if and only if the sky is not blue
Write the negation of p → q
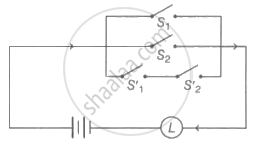
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
If q: There are clouds in the sky then p: it is raining. The symbolic form is ______
Which of the following is false?
Which of the following is NOT true for p → q.
Let S be a non-empty subset of R. Consider the following statement:
p: There is a rational number x ∈ S such that x > 0. Which of the following statements is the negation of the statement p?
The logical statement (∼p → q) ∧ (q → p) is equivalent to: ______
Let p, q and r be any three logical statements. Which of the following is true?
Which of the following is logically equivalent to `∼(∼p \implies q)`?
Converse of the statement q `rightarrow` p is ______.
From the following set of statements, select two statements which have similar meaning.
- If a man is judge, then he is honest.
- If a man is not a judge, then he is not honest.
- If a man is honest, then he is a judge.
- If a man is not honest, then he is not a judge.
Write the negation of (p `leftrightarrow` q).
Using truth table prove that:
~ (p `leftrightarrow` q) ≡ (p ∧ ~ q) ∨ (q ∧ ~ p)
Construct the truth table for the statement pattern:
[(p → q) ∧ q] → p
