Advertisements
Advertisements
प्रश्न
यदि चतुर्भुज ABCD के कोणों A, B, C और D का, इसी क्रम में लेने पर, अनुपात 3 : 7 : 6 : 4 है, तो ABCD है एक ______।
विकल्प
समचतुर्भुज
समांतर चतुर्भुज
समलंब
पतंग
उत्तर
यदि चतुर्भुज ABCD के कोणों A, B, C और D का, इसी क्रम में लेने पर, अनुपात 3 : 7 : 6 : 4 है, तो ABCD है एक समलंब।
स्पष्टीकरण -
प्रश्न में दिया गया है कि चतुर्भुज ABCD के कोणों का अनुपात 3 : 7 : 6 : 4 है।
माना चतुर्भुज ABCD के कोण क्रमशः 3x, 7x, 6x और 4x हैं।
इसलिए, 3x + 7x + 6x + 4x = 360° ...[चतुर्भुज के सभी कोणों का योग 360° है।]
20x = 360°
x = `(360^circ)/20`
x = 18°
इसलिए, चतुर्भुज के कोण हैं।
∠A = 3 × 18° = 54°
∠B = 7 × 18° = 126°
∠C = 6 × 18° = 108°
∠D = 4 × 18° = 72°
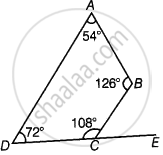
आकृति देखें, ∠BCE = 180° – ∠BCD ...[रैखिक युग्म अभिगृहीत]
∠BCE = 180° – 108° = 72°
∠BCE = ∠ADC = 72°
अब, BC || AD ...[संगत कोण बराबर हैं।]
सह आंतरिक कोणों का योग है -
∠A + ∠B = 126° + 54° = 180°
और ∠C + ∠D = 108° + 72° = 180°
अत:, ABCD एक समलंब है।
APPEARS IN
संबंधित प्रश्न
चतुर्भुज KLMN का एक रफ चित्र खींचिए। बताइए:
सम्मुख भुजाओं के दो युग्म
चतुर्भुज KLMN का एक रफ चित्र खींचिए। बताइए:
सम्मुख कोणों के दो युग्म
ABCD एक समचतुर्भुज है, जिसमें ∠ACB = 40° है। तब ∠ADB है
यदि चतुर्भुज ABCD के ∠A और ∠B के समद्विभाजक परस्पर P पर प्रतिच्छेद करते हैं, ∠B और ∠C के समद्विभाजक Q पर, ∠C और ∠D के R पर तथा ∠D और ∠A के S पर प्रतिच्छेद करते हैं, तो PQRS है एक ______।
यदि APB और CQD दो समांतर रेखाएँ हैं, तो कोणों APQ, BPQ, CQP और PQD के समद्विभाजक बनाते हैं
एक चतुर्भुज ABCD की भुजाओं के मध्य-बिंदुओं को, एक ही क्रम में, मिलाने पर प्राप्त आकृति केवल एक वर्ग है, यदि ______।
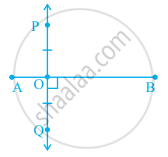
आकृति में, PQ ⊥ AB तथा PO = OQ है। क्या PQ रेखाखंड AB का लंब समद्विभाजक है? क्यों अथवा क्यों नहीं?
आकृति में, अधिक कोणों की संख्या है-

आकृति में
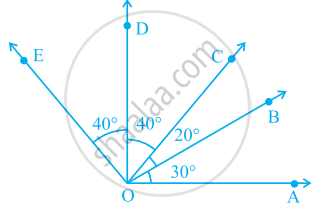
∠COA एक _____ कोण है।
आकृति में, 180° से छोटे कोणों की संख्या _____ है तथा इनके नाम ____ हैं।