Advertisements
Advertisements
प्रश्न
यदि एक बेलन की त्रिज्या दुगुनी कर दी जाए और उसकी ऊँचाई आधी कर दी जाए, तो उसका आयतन दुगुना हो जाएगा।
विकल्प
सत्य
असत्य
उत्तर
यह कथन सत्य है।
स्पष्टीकरण -
माना एक बेलन की त्रिज्या r तथा ऊँचाई h है।
फिर, एक बेलन का आयतन, V1 = πr2h
यदि एक बेलन की त्रिज्या, R = 2r
और एक बेलन की ऊंचाई, `H = h/2`
∴ बेलन का आयतन, V2 = πR2H
= `pi(2r)^2 h/2`
= 2πr2h
= 2 × V1
अत:, यदि एक बेलन की त्रिज्या दोगुनी कर दी जाए और एक बेलन की ऊंचाई आधी कर दी जाए, तो एक बेलन का आयतन दोगुना हो जाता है।
APPEARS IN
संबंधित प्रश्न
किसी मैदान को समतल करने के लिए 120 सेमी व्यास तथा 84 सेमी लंबाई वाले रोलर के 200 फेरे लगते हैं, तो 10 रु प्रतिवर्ग मीटर की दर से मैदान समतल करने में कितना खर्च लगेगा?
7 m त्रिज्या और 3 m ऊँचाई वाला एक बंद बेलनाकार टैंक किसी धातु की एक चादर से बना हुआ है। उसे बनाने के लिए वांछित धातु की चादर की मात्रा ज्ञात कीजिए।
किसी सड़क को समतल करने के लिए एक सड़क रोलर को सड़क के ऊपर एक बार घुमने के लिए 750 चक्कर लगाने पड़ते हैं। यदि सड़क रोलर का व्यास 84 cm और लंबाई 1 m है तो सड़क का क्षेत्रफल ज्ञात कीजिए।
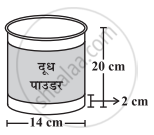
एक कंपनी अपने दूध पाउडर को ऐसे बेलनाकार बर्तनों में पैक करती है जिनका व्यास 14 cm और ऊँचाई 20 cm है। कंपनी बर्तन के पृष्ठ के चारों ओर एक लेबल लगाती है (जैसा कि आकृति में दर्शया गया है)। यदि यह लेबल बर्तन के तल और शीर्ष दोनों से 2 cm की दूरी पर चिपकाया जाता है तो लेबल का क्षेत्रफल क्या है?
दो बेलनों की त्रिज्याएँ 2 : 3 के अनुपात में हैं तथा उनकी ऊँचाईयों का अनुपात 5 : 3 है। उनके आयतनों का अनुपात है
10 m × 10 m × 5 m विमाओं वाले एक कमरे में रखे जा सकने वाले सबसे लंबे डंडे की लंबाई है
यदि एक बेलन की त्रिज्या दुगुनी कर दी जाए तथा उसके वक्र पृष्ठीय क्षेत्रफल में कोई परिवर्तन न किया जाए, तो उसकी ऊँचाई अवश्य ही आधी हो जाएगी।
एक बेलन और एक लंब वृत्तीय शंकु के समान आधार और समान ऊँचाई हैं। बेलन का आयतन शंकु के आयतन का तिगुना हैं।
2.5 m लंबे और 1.75 m त्रिज्या वाले एक बेलनाकार रोलर (roller) को जब सड़क पर रोल किया गया तो पाया गया कि उसने 5500 m2 के क्षेत्रफल को तय कर लिया है। रोलर ने कितने चक्कर लगा लिए थे?
एक वृत्ताकार लंब बेलन के आधार की त्रिज्या 20 सेमी तथा ऊँचाई 13 सेमी है तो उस वृत्ताकार लंब बेलन का वक्र पृष्ठफल तथा संपूर्ण पृष्ठफल ज्ञात कीजिए। (π = 3.14)
