Commerce (English Medium)
Science (English Medium)
Arts (English Medium)
Academic Year: 2021-2022
Date & Time: 6th December 2021, 11:30 am
Duration: 1h30m
Advertisements
General Instructions:
- This question paper comprises of 50 questions out of which 40 questions are to be attempted as per instructions. All questions carry equal marks,
- The question paper consists of three Sections - Section A, B and C.
- Section - A contains 20 questions. Attempt any 16 questions from Q. No. 1 to 20.
- Section - B also contains 20 questions. Attempt any 16 questions from Q. No. 21 to 40.
- Section - C contains 10 questions including one Case Study. Attempt any 8 questions from Q. No. 41 to 50.
- There is only one correct option for every Multiple Choice Question (MCQ). Marks will not be awarded for answering more than one option.
- There is no negative marking.
Differential of log [log (log x5)] w.r.t x is ______.
`5/(xlog(x^5)log(logx^5)`
`5/(xlog(logx^5)`
`(5x^4)/(log(x^5)log(logx^5)`
`(5x^4)/(logx^5log(logx^5)`
Chapter:
The number of all possible matrices of order 2 × 3 with each entry 1 or 2 is ______.
16
6
64
24
Chapter:
A function f : R `rightarrow` R is defined as f(x) = x3 + 1. Then the function has ______.
no minimum value
no maximum value
both maximum and minimum values
neither maximum value nor minimum value
Chapter:
If sin y = x cos(a + y), then `dx/dy` is ______.
`cosa/(cos^2(a + y))`
`(-cosa)/(cos^2(a + y))`
`cosa/(sin^2y)`
`(-cosa)/(sin^2y)`
Chapter:
The points on the curve `x^2/9 + y^2/25 = 1`, where tangent is parallel to X-axis are ______.
(±5, 0)
(0, ±5)
(0, ±3)
(±3, 0)
Chapter:
Three points P(2x, x + 3), Q(0, x) and R(x + 3, x + 6) are collinear, then x is equal to ______.
0
2
3
1
Chapter:
The principal value of `cos^-1(1/2) + sin^-1(-1/sqrt(2))` is ______.
`π/12`
π
`π/3`
`π/6`
Chapter:
If (x2 + y2)2 = xy, then `dy/dx` is ______.
`(y + 4x(x^2 + y^2))/(4y(x^2 + y^2) - x)`
`(y - 4x(x^2 + y^2))/(x + 4(x^2 + y^2))`
`(y - 4x(x^2 + y^2))/(4y(x^2 + y^2) - x)`
`(4y(x^2 + y^2) - x)/(y - 4x(x^2 + y^2))`
Chapter:
If a matrix A is both symmetric and skew symmetric, then A is necessarily a ______.
Diagonal matrix
Zero square matrix
Square matrix
Identity matrix
Chapter:
Let set X = {1, 2, 3} and a relation R is defined in X as: R = {(1, 3), (2, 2), (3, 2)}, then minimum ordered pairs which should be added in relation R to make it reflexive and symmetric are ______.
{(1, 1), (2, 3), (1, 2)}
{(3, 3), (3, 1), (1, 2)}
{(1, 1), (3, 3), (3, 1), (2, 3)}
{(1, 1), (3, 3), (3, 1), (1, 2)}
Chapter:
A Linear Programming Problem is as follows:
Minimise z = 2x + y
Subject to the constraints x ≥ 3, x ≤ 9, y ≥ 0
x – y ≥ 0, x + y ≤ 14
The feasible region has
5 corner points including (0, 0) and (9, 5)
5 corner points including (7, 7) and (3, 3)
5 corner points including (14, 0) and (9, 0)
5 corner points including (3, 6) and (9, 5)
Chapter:
The function `f(x) = {{:((e^(3x) - e^(-5x))/x",", if x ≠ 0),(k, if x = 0):}` is continuous at x = 0 for the value of k, as ______.
3
5
2
8
Chapter:
If Cij denotes the cofactor of element Pij of the matrix P = `[(1, -1, 2),(0, 2, -3),(3, 2, 4)]`, then the value of C31.C23 is ______.
5
24
–24
–5
Chapter:
The function y = x2e–x is decreasing in the interval
(0, 2)
(2, ∞)
(–∞, 0)
(–∞, 0) ∪ (2, ∞)
Chapter:
If R = {(x, y) : x, y ∈ Z, x2 + y2 ≤ 4} is a relation on Z, then the domain of R is ______.
{0, 1, 2}
{0, −1, −2}
{−2, −1, 0, 1, 2}
{−1, 0, 1}
None of these
Chapter:
The system of linear equations
5x + ky = 5,
3x + 3y = 5;
will be consistent if
k ≠ – 3
k = –5
k = 5
k ≠ 5
Chapter:
Advertisements
The equation of tangent to the curve y(1 + x2) = 2 – x, where it crosses x-axis is ______.
x + 5y = 2
x – 5y = 2
5x – y = 2
5x + y = 2
Chapter: [0.06] Applications of Derivatives
`[(3c + 6, a - d),(a + d, 2 - 3b)] = [(12, 2),(-8, -4)]` are equal, then value of ab – cd is ______.
4
16
–4
–16
Chapter:
The principal value of `tan^-1(tan (9π)/8)` is ______.
`π/8`
`(3π)/8`
`- π/8`
`- (3π)/8`
Chapter:
For two matrices P = `[(3, 4),(-1, 2),(0, 1)]` and QT = `[(-1, 2, 1),(1, 2, 3)]` P – Q is ______.
`[(2, 3),(-3, 0),(0, -3)]`
`[(4, 3),(-3, 0),(-1, -2)]`
`[(4, 3),(-0, -3),(-1, -2)]`
`[(2, 3),(0, -3),(0, -3)]`
Chapter:
The function f(x) = 2x3 – 15x2 + 36x + 6 is increasing in the interval
(–∞, 2) ∪ (3, ∞)
(–∞, 2)
(–∞, 2] ∪ [3, ∞)
[3, ∞)
Chapter:
If x = 2 cos θ – cos 2θ and y = 2 sin θ – sin 2θ, then `dy/dx` is ______.
`(cosθ + cos2θ)/(sinθ - sin2θ_`
`(cosθ - cos2θ)/(sin2θ - sinθ)`
`(cosθ - cos2θ)/(sinθ - sin2θ)`
`(cos2θ - cosθ)/(sin2θ + sinθ)`
Chapter:
What is the domain of the function cos–1 (2x – 3)?
[–1, 1]
(1, 2)
(–1, 1)
[1, 2]
Chapter:
A matrix A = [aij]3 × 3 is defined by
`a_(ij) = {{:(2i + 3j",", i < j),(5",", i = j),(3i - 2j",", i > j):}`
The number of elements in A which are more than 5, is ______.
3
4
5
6
Chapter:
If a function f defined by
`f(x) = {{:((k cos x)/(π - 2x)",", if x ≠π/2),(3, if x = π/2):}`
is continuous at `x = π/2`, then the value of k is ______.
2
3
6
–6
Chapter:
For the matrix `X = [(0, 1, 1),(1, 0, 1),(1, 1, 0)], (X^2 - X)` is ______.
2I
3I
I
5I
Chapter:
Let X = {x2 : x ∈ N} and the function f : N `rightarrow` X is defined by f(x) = x2, x ∈ N. Then this function is ______.
injective only
not bijective
surjective only
bijective
Chapter:
The corner points of the feasible region for a Linear Programming problem are P(0, 5), Q(1, 5), R(4, 2) and S(12, 0). The minimum value of the objective function Z = 2x + 5y is at the point ______.
P
Q
R
S
Chapter:
The equation of the normal to the curve ay2 = x3 at the point (am2, am3) is ______.
2y – 3mx + am3 = 0
2x + 3my 3am4 – am2 = 0
2x + 3my + 3am4 – 2am = 0
2x + 3my – 3am4 – 2am2 = 0
Chapter:
If A is a square matrix of order 3 and |A| = –5, then |adj A| is ______.
125
–25
25
±25
Chapter:
The simplest form of `tan^-1 [(sqrt(1 + x) - sqrt(1 - x))/(sqrt(1 + x) + sqrt(1 - x))]` is ______.
`π/4 - x/2`
`π/4 + x/2`
`π/4 - 1/2 cos^-1x`
`π/4 + 1/2 cos^-1x`
Chapter:
If for the matrix A = `[(α, -2),(-2, α)]`, |A3| = 125, then the value of α is ______.
±3
–3
±1
1
Chapter:
Advertisements
If y = sin (msin–1x), then which one of the following equations is true?
`(1 - x^2) (d^2y)/(dx^2) + x dy/dx + m^2y = 0`
`(1 - x^2) (d^2y)/(dx^2) - x dy/dx + m^2y = 0`
`(1 + x^2) (d^2y)/(dx^2) - x dy/dx - m^2y = 0`
`(1 + x^2) (d^2y)/(dx^2) + x dy/dx - m^2x = 0`
Chapter:
The principal value of `[tan^-1sqrt(3) - cot^-1(-sqrt(3))]` is ______.
π
`-π/2`
0
`2sqrt(3)`
Chapter:
The maximum value of `(1/x)^x` is ______.
e
ex
`"e"^(1/"e")`
`(1/"e")^(1/"e")`
ee
Chapter: [0.06] Applications of Derivatives
Let matrix X = [xij] is given by X = `[(1, -1, 2),(3, 4, -5),(2, -1, 3)]`. Then the matrix Y = [mij], where mij = Minor of xij, is ______.
`[(7, -5, -3),(19, 1, -11),(-11, 1, 7)]`
`[(7, -19, 11),(5, -1, -1),(3, 11, 7)]`
`[(7, 19, -11),(-3, 11, 7),(-2, -1, -1)]`
`[(7, 19, -11),(-1, -1, 1),(-3, -11, 7)]`
Chapter:
A function f : R `rightarrow` R defined by f(x) = 2 + x2 is ______.
not one-one
one-one
not onto
neither one-one nor onto
Chapter:
A Linear Programming Problem is as follows:
Maximise / Minimise objective function
Z = 2x – y + 5
Subject to the constraints
3x + 4y ≤ 60
x + 3y ≤ 30
x ≥ 0, y ≥ 0
If the corner points of the feasible region are A(0, 10), B(12, 6), C(20, 0) and O(0, 0), then which of the following is true?
Maximum value of Z is 40
Minimum value of Z is –5
Difference of maximum and minimum values of Z is 35
At two corner points, value of Z are equal
Chapter:
If x = –4 is a root of `|(x, 2, 3),(1, x, 1),(3, 2, x)| = 0`, then the sum of the other two roots is ______.
4
–3
2
5
Chapter:
The absolute maximum value of the function `f(x) = 4x - 1/2 x^2` in the interval `[-2, 9/2]` is ______.
8
9
6
10
Chapter:
In a sphere of radius r, a right circular cone of height h having maximum curved surface area is inscribed. The expression for the square of curved surface of cone is ______.
2π2rh(2rh + h2)
π2hr(2rh + h2)
2π2r(2rh2 – h3)
2π2r2(2rh – h2)
Chapter:
The corner points of the feasible region determined by a set of constraints (linear inequalities) are P(0, 5), Q(3, 5), R(5, 0) and S(4, 1) and the objective function is Z = ax + 2by where a, b > 0. The condition on a and b such that the maximum Z occurs at Q and S is ______.
a – 5b = 0
a – 3b = 0
a – 2b = 0
a – 8b = 0
Chapter:
If curves y2 = 4x and xy = c cut at right angles, then the value of c is ______.
`4sqrt(2)`
8
`2sqrt(2)`
`-4sqrt(2)`
Chapter:
The inverse of the matrix X = `[(2, 0, 0),(0, 3, 0),(0, 0, 4)]` is ______.
`24[(1//2, 0, 0),(0, 1//3, 0),(0, 0, 1//4)]`
`1/24[(1, 0, 0),(0, 1, 0),(0, 0, 1)]`
`1/24[(2, 0, 0),(0, 3, 0),(0, 0, 4)]`
`[(1//2, 0, 0),(0, 1//3, 0),(0, 0, 1//4)]`
Chapter:
For an L.P.P. the objective function is Z = 4x + 3y and the feasible region determined by a set of constraints (linear inequations) is shown in the graph.
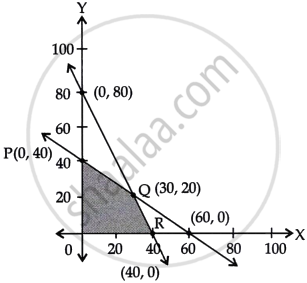
Which one of the following statements is true?
Maximum value of Z is at R.
Maximum value of Z is at Q.
Value of Z at R is less than the value at P.
Value of Z at Q is less than the value at R.
Chapter:
|
Case Study In a residential society comprising of 100 houses, there were 60 children between the ages of 10-15 years. They were inspired by their teachers to start composting to ensure that biodegradable waste is recycled. For this purpose, instead of each child doing it for only his/her house, children convinced the Residents welfare association to do it as a society initiative. For this they identified a square area in the local park. Local authorities charged amount of ₹ 50 per square metre for space so that there is no misuse of the space and Resident welfare association takes it seriously. Association hired a labourer for digging out 250 m3 and he charged ₹ 400 X (depth)2. Association will like to have minimum cost.
|
Let side of square plot is x m and its depth is h metres, then cost C for the pit is
`50/h + 400h^2`
`12500/h + 400h^2`
`250/h + h^2`
`250/h + 400h^2`
Chapter:
|
Case Study In a residential society comprising of 100 houses, there were 60 children between the ages of 10-15 years. They were inspired by their teachers to start composting to ensure that biodegradable waste is recycled. For this purpose, instead of each child doing it for only his/her house, children convinced the Residents welfare association to do it as a society initiative. For this they identified a square area in the local park. Local authorities charged amount of ₹ 50 per square metre for space so that there is no misuse of the space and Resident welfare association takes it seriously. Association hired a labourer for digging out 250 m3 and he charged ₹ 400 X (depth)2. Association will like to have minimum cost.
|
Value of h (in m) for which `(dC)/(dh) = 0` is
1.5
2
2.5
3
Chapter:
|
Case Study In a residential society comprising of 100 houses, there were 60 children between the ages of 10-15 years. They were inspired by their teachers to start composting to ensure that biodegradable waste is recycled. For this purpose, instead of each child doing it for only his/her house, children convinced the Residents welfare association to do it as a society initiative. For this they identified a square area in the local park. Local authorities charged amount of ₹ 50 per square metre for space so that there is no misuse of the space and Resident welfare association takes it seriously. Association hired a labourer for digging out 250 m3 and he charged ₹ 400 X (depth)2. Association will like to have minimum cost.
|
`(d^2C)/(dh^2)` is given by
`25000/h^3 + 800`
`500/h^3 + 800`
`100/h^3 + 800`
`500/h^3 + 2`
Chapter:
|
Case Study In a residential society comprising of 100 houses, there were 60 children between the ages of 10-15 years. They were inspired by their teachers to start composting to ensure that biodegradable waste is recycled. For this purpose, instead of each child doing it for only his/her house, children convinced the Residents welfare association to do it as a society initiative. For this they identified a square area in the local park. Local authorities charged amount of ₹ 50 per square metre for space so that there is no misuse of the space and Resident welfare association takes it seriously. Association hired a labourer for digging out 250 m3 and he charged ₹ 400 X (depth)2. Association will like to have minimum cost.
|
Value of x (in m) for minimum cost is
5
`10sqrt(5/3)`
`5sqrt(5)`
10
Chapter:
|
Case Study In a residential society comprising of 100 houses, there were 60 children between the ages of 10-15 years. They were inspired by their teachers to start composting to ensure that biodegradable waste is recycled. For this purpose, instead of each child doing it for only his/her house, children convinced the Residents welfare association to do it as a society initiative. For this they identified a square area in the local park. Local authorities charged amount of ₹ 50 per square metre for space so that there is no misuse of the space and Resident welfare association takes it seriously. Association hired a labourer for digging out 250 m3 and he charged ₹ 400 X (depth)2. Association will like to have minimum cost.
|
Total minimum cost of digging the pit (in ₹) is
4,100
7,500
7,850
3,220
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 12 Mathematics with solutions 2021 - 2022
Previous year Question paper for CBSE Class 12 Maths-2022 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 12.
How CBSE Class 12 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.

