Advertisements
Advertisements
Draw ∠ABC of measure 105° and bisect it.
Concept: Basic Geometric Constructions
Write down the equation of a line whose slope is 3/2 and which passes through point P, where P divides the line segment AB joining A(-2, 6) and B(3, -4) in the ratio 2 : 3.
Concept: Division of a Line Segment
ΔRST ~ ΔUAY, In ΔRST, RS = 6 cm, ∠S = 50°, ST = 7.5 cm. The corresponding sides of ΔRST and ΔUAY are in the ratio 5 : 4. Construct ΔUAY.
Concept: Division of a Line Segment
Construct the circumcircle and incircle of an equilateral ∆XYZ with side 6.5 cm and centre O. Find the ratio of the radii of incircle and circumcircle.
Concept: Division of a Line Segment
Draw a circle with centre O and radius 3.5 cm. Take point P at a distance 5.7 cm from the centre. Draw tangents to the circle from point P.
Concept: Construction of a Tangent to the Circle at a Point on the Circle
Prove that “That ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.”
Concept: Basic Geometric Constructions
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Concept: To Construct Tangents to a Circle from a Point Outside the Circle.
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
Concept: General Equation of a Line
Find the slope and y-intercept of the line y = -2x + 3.
Concept: Intercepts Made by a Line
Write down the equation of a line whose slope is 3/2 and which passes through point P, where P divides the line segment AB joining A(-2, 6) and B(3, -4) in the ratio 2 : 3.
Concept: Division of a Line Segment
ΔRST ~ ΔUAY, In ΔRST, RS = 6 cm, ∠S = 50°, ST = 7.5 cm. The corresponding sides of ΔRST and ΔUAY are in the ratio 5 : 4. Construct ΔUAY.
Concept: Division of a Line Segment
Find the slope and y – intercept of the line y = 3x – 5.
Concept: Intercepts Made by a Line
Construct the circumcircle and incircle of an equilateral ∆XYZ with side 6.5 cm and centre O. Find the ratio of the radii of incircle and circumcircle.
Concept: Division of a Line Segment
A (5, 4), B (–3,–2) and C (1,–8) are the vertices of a triangle ABC. Find the equation of median AD and line parallel to AB passing through point C.
Concept: General Equation of a Line
Find the coordinates of midpoint of the segment joining the points (22, 20) and (0, 16).
Concept: The Mid-point of a Line Segment (Mid-point Formula)
Find the Slope of the line having inclination 45°.
Concept: Slope of a Line
Find distance between point Q(3, – 7) and point R(3, 3)
Solution: Suppose Q(x1, y1) and point R(x2, y2)
x1 = 3, y1 = – 7 and x2 = 3, y2 = 3
Using distance formula,
d(Q, R) = `sqrt(square)`
∴ d(Q, R) = `sqrt(square - 100)`
∴ d(Q, R) = `sqrt(square)`
∴ d(Q, R) = `square`
Concept: Distance Formula
If the angle θ= –60º, find the value of cosθ.
Concept: Trigonometric Ratios of Complementary Angles
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
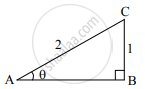
Concept: Heights and Distances
Prove that sin6θ + cos6θ = 1 – 3 sin2θ. cos2θ.
Concept: Trigonometric Identities
