Advertisements
Advertisements
प्रश्न
A(5, x), B(−4, 3) and C(y, –2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.
उत्तर
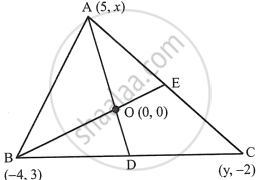
Co-ordinates of centroid of ΔABC are (0, 0)
∴ `0 = (x_1 + x_2 + x_3)/3`
= `(5 - 4 + y)/3`
`=> 0 = (y + 1)/3`
`=>` y + 1 = 0
∴ y = –1
Again `0 = (y_1 + y_2 + y_3)/3`
= `(x + 3 - 2)/3`
`=> 0 = (x + 1)/3`
`=>` x + 1 = 0
∴ x = –1
∴ x = –1, y = –1
APPEARS IN
संबंधित प्रश्न
The co-ordinates of the centroid of a triangle PQR are (2, –5). If Q = (–6, 5) and R = (11, 8); calculate the co-ordinates of vertex P.
Find the coordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
Point P is the midpoint of seg AB. If co-ordinates of A and B are (-4, 2) and (6, 2) respectively then find the co-ordinates of point P.
(A) (-1,2) (B) (1,2) (C) (1,-2) (D) (-1,-2)
Two vertices of a triangle are (1, 4) and (3, 1). If the centroid of the triangle is the origin, find the third vertex.
A(3, 1), B(y, 4) and C(1, x) are vertices of a triangle ABC. P, Q and R are mid - points of sides BC, CA and AB respectively. Show that the centroid of ΔPQR is the same as the centroid ΔABC.
As shown in the figure. two concentric circles are given and line AB is the tangent to the smaller circle at T. Shown that T is the midpoint of Seg AB
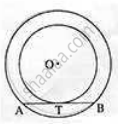
Point M is the mid-point of segment AB. If AB = 8.6 cm, then find AM.
If (1, −2), (3, 6), (x, 10) and (3, 2) are the vertices of the parallelogram taken in order, then the value of x is
From the figure given alongside, find the length of the median AD of triangle ABC. Complete the activity.
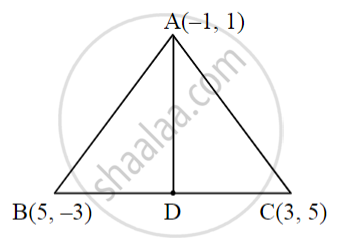
Solution:
Here A(–1, 1), B(5, – 3), C(3, 5) and suppose D(x, y) are coordinates of point D.
Using midpoint formula,
x = `(5 + 3)/2`
∴ x = `square`
y = `(-3 + 5)/2`
∴ y = `square`
Using distance formula,
∴ AD = `sqrt((4 - square)^2 + (1 - 1)^2`
∴ AD = `sqrt((square)^2 + (0)^2`
∴ AD = `sqrt(square)`
∴ The length of median AD = `square`
Find the coordinates of the mid-point of the line segment with points A(– 2, 4) and B(–6, –6) on both ends.
